RD-V: 0020 Cantilever Beam

Deflection of a cantilever beam modeled with different meshes and different element formulations.

The subject of this study is to analyze the quality of Radioss quasi-linear simulation using a simple use case. This should give an overview about the trade-off between quality and performance with respect to different modeling techniques. This example deals with the use of the Radioss nonlinear solver.

Based on a well-known small example from literature, the set-up of a simple Radioss input deck for a linear-elastic application will be shown: the cantilever-beam.

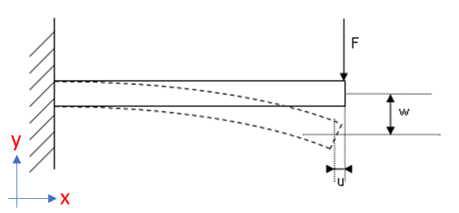
The beam is clamped at one end, and loaded with a concentrated force on the other end. The maximum vertical deflection is used for results comparison. This problem is well understood, and results can be easily compared with an analytical solution.

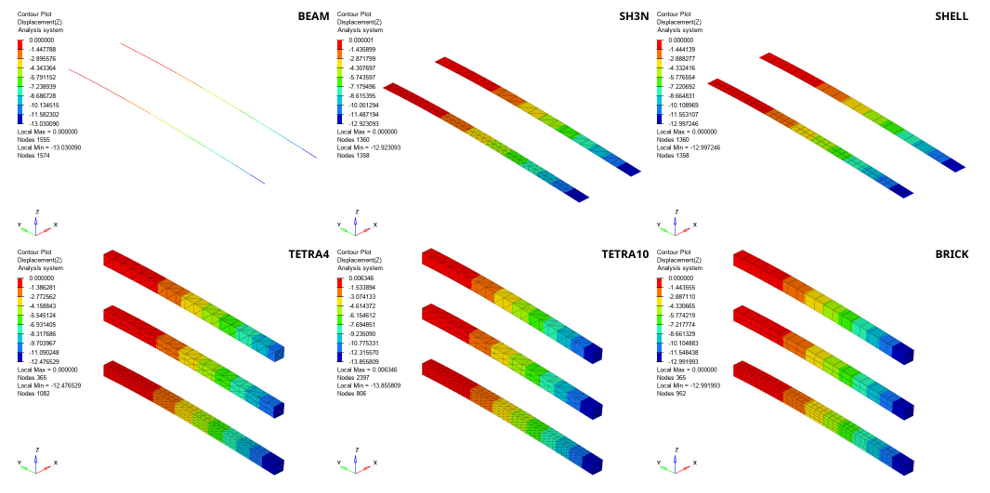
In this example, different mesh techniques are compared: beams, 3 and 4 noded shells, hexahedral elements and tetrahedral (tetra4 and tetra10) elements, as well as different element sizes.

The results are extracted and compared between each other with respect to their mesh size and element formulation. As output, the maximum vertical deflection, number of cycles, calculation time, element stress, and overall error are used. The maximum vertical deflection is compared to the theoretical value.

Options and Keywords Used

/MAT/LAW1 (ELAST)
/PROP/TYPE1 (SHELL)
/PROP/TYPE3 (BEAM)
/PROP/TYPE14 (SOLID)
/TETRA4
/TETRA10
/BEAM
/BRICK
/SHELL
/SH3N
/CLOAD
/FUNCT_SMOOTH
Mesh density

Input Files

Before you begin, copy the file(s) used in this problem to your working directory.

RD-V-0020_Cantilever_Beam.zip

モデル概要

この例は、シンプルな片持ち梁向けの各種モデリング手法を、品質とパフォーマンスの点で比較することを目的としています。

片持ち梁は左端で固定されており、右端には集中荷重がかけられています。

用いられた材料は線形弾性則（/MAT/LAW1）に従い、以下の特性を持ちます。

初期密度: 7.8 x 10^-9 [Mg/mm³]
ヤング率: 210000 [MPa]
ポアソン比: 0.3
板厚: 10 [mm]
長さ: 190 [mm]
幅: 10 [mm]
荷重ケース: Fx = 0; Fy = -1000.0; Fz = 0

この線形問題では、解析解で次の式が得られます：

w = \frac{F L^{3}}{3 E I}

ここで、

$F$: 力
$L$: 梁の長さ
$E$: ヤング率
$I$: 慣性モーメント

理論的なたわみはw = 13.07mmと決定されます。

シミュレーションの反復

梁は6種類の要素でモデル化されています：

/BEAM
/SH3N
/SHELL
/BRICK
/TETRA4
/TETRA10

それぞれの定式化には特定のプロパティ（/PROP）があります。/PROP/TYPE3 (BEAM)は、ねじれ、曲げ、膜、または軸の変形のビームプロパティを記述します。ビーム要素では、デフォルトの非線形ひずみ定式化（I_smstr = 4）が使用されます。さらに、次の設定を行う必要があります。

断面積: 100 mm²
慣性モーメント（曲げ）: 833.33333 mm⁴
慣性モーメント（ねじれ）: 1666.66666 mm⁴

シェル要素（/PROP/TYPE1 (SHELL)）の場合、QBAT-shell（I_shell = 12）とQEPH-shell（I_shell = 24）という2つの要素定式化が使用されます。

３次元ソリッド要素（/PROP/TYPE14 (SOLID)）の場合、I_solid = 14、17、18、24というソリッド定式化が調査されます。

Tetra4要素の場合、I_tetra4 = 0、1、3という定式化が使用され、Tetra10要素の場合、I_tetra10 = 0、2という定式化が使用されます。

変位が微小で、線形ソルバーを使用できても、非線形の陽解法および陰解法ソルバーが使用されます。非線形陰解法ソルバーをアクティブにするには、/IMPL/NONLINを使用します。

Results

The tables below provide an overview about maximum deflection in Z-direction compared to the theoretical result. The results are compared between each other with respect to their mesh size, total number of cycles, energy error and difference of deflection compared to the theoretical value. The explicit CPU costs are normalized with respect to the QEPH shell simulation running on a single CPU and should be considered approximate. For Implicit calculation the CPU costs are similar for all element types. The displacement results in the table are reported at the main node of the rigid body attached to the end of the beam where the force is applied.

Explicit Solver

表 1. Explicit Results of Deflection of a Cantilever Beam Modeled with Beams and Shell Elements
Element	Mesh Size [mm]	Element Formulation	Maximum Deflection in Z-Direction [mm]	CPU Cost Factor (vs QEPH Shells)	Total Number of Cycles	Difference to Theoretical value [%]
BEAM	10	BEAMN3	13.03	1.3	255801	0.3
BEAM	5	BEAMN3	13.03	1.3	255801	0.3
SH3N	10	`I`_sh3n=0,2	12.919	1.7	245758	1.2
SH3N	5	`I`_sh3n=0,2	12.981	1.7	245758	0.7
SH3N	10	`I`_sh3n=30	12.903	3.3	450006	1.3
SH3N	5	`I`_sh3n=30	12.923	3.3	450006	1.1
QBAT	10	`I`_shell = 12 BATOZ	12.885	1.7	139698	1.4
QBAT	5	`I`_shell = 12 BATOZ	12.946	1.7	139698	0.9
QEPH	10	`I`_shell = 24 QEPH	12.975	1.0	137169	0.7
QEPH	5	`I`_shell = 24 QEPH	12.997	1.0	137169	0.6

表 2. Explicit Results of Deflection of a Cantilever Beam Modeled with Tetra4 and Tetra10 Elements
Element	Mesh Size [mm]	Element Formulation	Maximum Deflection in Z-Direction [mm]	CPU Cost Factor (vs QEPH Shells)	Total Number of Cycles	Difference to Theoretical value [%]
TETRA4	10	`I`_tetra4 = 0	3.633	8.1	344287	72.2
	5		5.245			59.9
	2.5		9.171			29.8
TETRA4	10	`I`_tetra4 = 1	10.324	29.9	344277	21.0
	5		11.231			14.1
	2.5		12.452			4.7
TETRA4	10	`I`_tetra4 = 3	5.259	8.9	344255	59.8
	5		6.003			54.1
	2.5		9.743			25.5
TETRA10	10	`I`_tetra10 = 0	13.341	113.9	1301767	2.1
	5		13.824			5.8
	2.5		13.613			4.2
TETRA10	10	`I`_tetra10 = 2	13.341	46.1	478817	2.3
	5		13.824			5.8
	2.5		13.613			4.2

表 3. Explicit Results of Deflection of a Cantilever Beam Modeled with Hexa8 Elements
Element	Mesh Size [mm]	Element Formulation	Maximum Deflection in Z-Direction [mm]	CPU Cost Factor (vs QEPH Shells)	Total Number of Cycles	Difference to Theoretical value [%]
BRICK	10	`I`_solid = 14	12.964	11.9	281572	0.8
	5		12.890			1.4
	2.5		12.939			1.0
BRICK	10	`I`_solid = 17	15.682	9.3	281584	20.0
	5		9.910			24.2
	2.5		11.985			8.3
BRICK	10	`I`_solid = 18	12.964	14.5	281572	0.8
	5		12.890			1.4
	2.5		12.939			1.0
BRICK	10	`I`_solid = 24 HEPH	12.966	4.1	281558	0.8
	5		12.890			1.4
	2.5		12.939			1.0

Implicit Solver

表 4. Implicit Results of Deflection of a Cantilever Beam Modeled with Beams and Shell Elements
Element	Mesh Size [mm]	Element Formulation	Maximum Deflection in Z-Direction [mm]	Total Number of Cycles	Difference to Theoretical value [%]
BEAM	10	BEAMN3	13.032	12	0.3
BEAM	5	BEAMN3	13.032	12	0.3
SH3N	10	`I`_sh3n=0	12.909	15	1.2
SH3N	5	`I`_sh3n=0	13.614	15	4.2
SHELL	10	`I`_shell = 12 BATOZ	12.951	15	0.9
SHELL	5	`I`_shell = 12 BATOZ	12.975	15	0.7
SHELL	10	`I`_shell = 24 QEPH	12.958	13	0.9
SHELL	5	`I`_shell = 24 QEPH	12.976	13	0.7

表 5. Implicit Results of Deflection of a Cantilever Beam Modeled with Tetra4 and Tetra10 Elements
Element	Mesh Size [mm]	Element Formulation	Maximum Deflection in Z-Direction [mm]	Total Number of Cycles	Difference to Theoretical value [%]
TETRA4	10	`I`_tetra4 = 0	3.633	12	72.2
	5		5.244		59.9
	2.5		9.172		29.8
TETRA10	10	`I`_tetra10 = 0	13.336	16	2.0
	5		13.819		5.7
	2.5		13.608		4.1

表 6. Implicit Results of Deflection of a Cantilever Beam Modeled with Hexa8 Elements
Element	Mesh Size [mm]	Element Formulation	Maximum Deflection in Z-Direction [mm]	Total Number of Cycles	Difference to Theoretical value [%]
BRICK	10	`I`_solid = 14	12.965	15	0.8
	5		12.890		1.4
	2.5		12.939		1.0
BRICK	10	`I`_solid = 17	15.673	16	19.9
	5		9.908		24.2
	2.5		11.981		8.3
BRICK	10	`I`_solid = 18	12.964	18	0.8
	5		12.890		1.4
	2.5		12.939		1.0
BRICK	10	`I`_solid = 24 HEPH	12.966	15	0.8
	5		12.890		1.4
	2.5		12.939		1.0

Conclusion

Explicit Solver
Beam: BEAM3N returns good results for the coarse and the fine mesh. The difference of deflection compared to the theoretical value is about 0.2%.
Shells: When the beam is modeled with 4 node shell elements, QEPH (I_shell = 24) is the best choice of element formulation. Compared to QBAT (I_shell = 12), it returns similar results regarding mesh size, energy error, with very good precision versus cost.; Both 3 node shell element formulations, default (I_sh3n = 0) and DKT18 (I_sh3n = 30), return similar results, close to the theoretical value. I_sh3n = 30 is almost twice as computationally expensive as I_sh3n = 0.
Tetras: I_tetra4 = 0 or 3 elements are too stiff and do not return reasonable results, unless a fine mesh is used. Although, having a higher computational cost, the I_tetra4 = 1 element formulation returns better results especially when a fine mesh is used.; Tetra10 elements returns good results, but with a significantly higher calculation time compared to tetra4 elements. The I_tetra10 = 2 formulation return the same results as the I_tetra10 = 0 formulation, but with half the computational cost.
Bricks: Hexa8 elements with I_solid = 24 element formulation return the best results regarding mesh size, and calculation time. They also have very good precision versus cost ratio. The difference of deflection compared to the theoretical value is about 1%. Compared to the other brick element formulations calculation time is about 2 – 2.5 lower. When used with nonlinear materials, I_solid = 24 requires 3 or more elements through the thickness. For 1 or 2 elements through the thickness, a fully-integrated element, like I_solid = 14 or 18 is recommended. The I_solid = 18 element automatically selects the best property settings depending on the material it is used with. The fully-integrated I_solid = 17 element suffers from shear locking which causes it to be too stiff and therefore not recommended.

Implicit Solver
Beam: BEAM3N returns good results for the coarse and the fine mesh. The difference of deflection compared to the theoretical value is about 0.3%.
Shells: Shell elements with different element formulations return good results regarding mesh size and calculation time. The difference of deflection to the theoretical value is under 1%. The QEPH shell shows best performance versus precision ratio and is recommended.; The 3 node shell elements I_sh3n = 0 returns results close to the theoretical value.
Tetras: Tetra10 elements return good results in terms of quality compared to tetra4 elements, which are too stiff in their behavior. The difference of deflection compared to the theoretical value varies between 2 to 6% and depends on the mesh size. For Tetra4 elements, the deflection compared to the theoretical value is to low, but begins to converge with finer mesh size. The I_tetra4 = 1 and I_tetra10 = 2 element formulations are not supported in implicit analysis.
Bricks: Hexa8 elements with different element formulations return good results for the coarse and the fine mesh, except for element formulation I_solid = 17 which suffers from shear locking. The difference of deflection compared to the theoretical value is about 1%. The Hexa8 elements with I_solid = 24 show the best performance regarding precision of results and calculation time.