RMS2
Computes the root mean square area difference between a measured signal and a target curve.
Example
Assume that you are designing a planar four bar mechanism. You want a metric that accurately represents the deviation of the X-coordinate of the CM of the coupler link from a desired profile. The RMS2 response will capture the required deviation metric.
The desired profile for the X-coordinate of the CM of the coupler link is as follows:
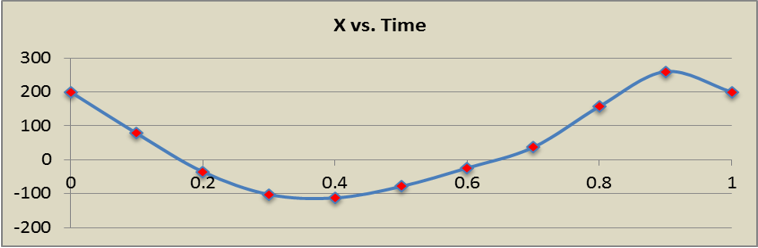
[(0.0, 199.997),
(0.1, 78.0588),
(0.2, -35.233),
(0.3, -102.140),
(0.4, -112.560),
(0.5, -78.718),
(0.6, -23.994),
(0.7, 36.862),
(0.8, 157.392),
(0.9, 260.213),
(1.0, 199.997)]
Here is a code snippet that will compute the RMS2 response for the X-coordinate of the CM of the coupler link coupler.
>>> # Define the X vs. Time profile
>>> xy = [(0.0, 199.997),
(0.1, 78.0588),
(0.2, -35.233),
(0.3, -102.140),
(0.4, -112.560),
(0.5, -78.718),
(0.6, -23.994),
(0.7, 36.862),
(0.8, 157.392),
(0.9, 260.213),
(1.0, 199.997)]
>>>
>>> # Define the signal to be measured
>>> dx_coupler = "DX ({})".format(coupler.cm.id)
>>>
>>> # Define the RMS2 response
>>> rms2x = RMS2 (label = "Coupler-DX", targetValue = xy, measuredValue = dx_coupler)The calculations in RMS2 for this example are implemented as follows:
X = (0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)
Y = (199.997, 78.058, -35.233, -102.140, -112.560, -78.718, -23.994, 36.862, 157.392, 260.213, 199.997)
Spline = Spline (x=x, y=y)
Response =
X = (0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)
Y = (199.997, 78.058, -35.233, -102.140, -112.560, -78.718, -23.994,
36.862, 157.392, 260.213, 199.997)
Spline = Spline (x=x, y=y)
Response =