CRASURV Formulation (I_form= 1)

Format

Definition

Comments

1. The formulation flag I_form should be set to 1, for the CRASURV (crash survivability) formulation. Compare with I_form=0, in this formulation:
   • The F variable coefficients of $\mathrm{F}(\sigma )$ is function of plastic work and strain rate
   • It allows the simulation of the ductile failure of orthotropic shells
   • Considering different plastic and failure behaviors in tension, in compression and in shear
2. Usage with property and element type.
   • This material requires orthotropic shell properties (/PROP/TYPE9 (SH_ORTH), /PROP/TYPE10 (SH_COMP) or /PROP/TYPE11 (SH_SANDW)). These properties specify the orthotropic direction, therefore, it is not compatible with the isotropic shell property (/PROP/TYPE1 (SHELL)). Property /PROP/SH_ORTH is not compatible with the CRASURV formulation.
   • This material is available with under-integrated Q4 (I_shell= 1,2,3,4) and fully integrated BATOZ (I_shell=12) shell formulations.
   • This material is compatible with orthotropic solid property (/PROP/SOL_ORTH), the orthotropic thick shell property (/PROP/TSH_ORTH) and the composite thick shell property (/PROP/TSH_COMP). These properties specify the orthotropic directions. It is assumed that, for solids and thick shells, the material is elastic and the E₃₃ value must be set in such cases.
   • Failure criterion in LAW25 is not applicable to solid elements. To determine failure for solid elements /FAIL card should be used.
   • For shell and thick shell composite parts, with /PROP/SH_COMP, /PROP/SH_SANDW, /PROP/TSH_ORTH or /PROP/TSH_COMP, material is defined directly in the property card. The failure criteria defined within this material (for example, LAW25) are accounted for. Material referred to in the corresponding /PART card is not used.
3. The Tsai-Wu criterion:
   The material is assumed to be elastic until the Tsai-Wu criterion is fulfilled:

   • If $\mathrm{F}(\sigma )<1$ : Elastic
   • If $\mathrm{F}(\sigma )>1$ : Nonlinear

   Where, $\mathrm{F}(\sigma )$ is stress in element for Tsai-Wu criterion, is computed as:

   $$\mathrm{F}(\sigma )=F_1{\sigma }_1+F_2{\sigma }_2+F_{11}{\sigma }_1^2+F_{22}{\sigma }_2^2+2F_{12}{\sigma }_1{\sigma }_2+F_{44}{\sigma }_{12}^2$$

   Here, ${\sigma }_1$ , ${\sigma }_2$ and ${\sigma }_{12}$ are the stresses in the material coordinate system.

   The F variable coefficients of $\mathrm{F}(\sigma )$ for Tsai-Wu criterion is functions of plastic work $\mathrm{F}\left(W_p^{*}·\dot{\epsilon }\right)$ and is determined as:

   $$F_i\left(W_p^{*},\dot{\epsilon }\right)=-\frac{1}{{\sigma }_i^c\left(W_p^{*},\dot{\epsilon }\right)}+\frac{1}{{\sigma }_i^t\left(W_p^{*},\dot{\epsilon }\right)}$$
   $$F_{ii}\left(W_p^{*},\dot{\epsilon }\right)=\frac{1}{{\sigma }_i^c\left(W_p^{*},\dot{\epsilon }\right)\cdot {\sigma }_i^t\left(W_p^{*},\dot{\epsilon }\right)}$$
   $$F_{12}\left(W_p^{*},\dot{\epsilon }\right)=-\frac{\alpha }{2}\sqrt{F_{11}\left(W_p^{*},\dot{\epsilon }\right)F_{22}\left(W_p^{*},\dot{\epsilon }\right)}$$
   $$F_{44}\left(W_p^{*},\dot{\epsilon }\right)=\frac{1}{{\sigma }_{12}^{}\left(W_p^{*},\dot{\epsilon }\right)\cdot {\sigma }_{12}^{}\left(W_p^{*},\dot{\epsilon }\right)}$$

   Where, $i$ =1 or 2.

   The values of the limiting stresses when the material becomes nonlinear in directions 1, 2 or 12 (shear) are modified based on the values of plastic work and strain rate, as:

   In tension:

   $${\sigma }_i^t\left(W_p^{*},\dot{\epsilon }\right)\text{=}{\sigma }_{iy}^t\left(1+b_i^t{(W_p^{*})}^{n_i^t}\right)\left(1+c_i^t\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$$

   Where, $i$ =1 or 2.

   In compression:

   $${\sigma }_i^c\left(W_p^{*},\dot{\epsilon }\right)\text{=}{\sigma }_{iy}^c\left(1+b_i^c{(W_p^{*})}^{n_i^c}\right)\left(1+c_i^c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$$

   Where, $i$ =1 or 2.

   In shear:

   $${\sigma }_{12}^{}\left(W_p^{*},\dot{\epsilon }\right)\text{=}{\sigma }_{12y}^{}\left(1+b_{12}^{}{(W_p^{*})}^{n_{12}^{}}\right)\left(1+c_{12}^{}\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$$

   The superscripts $c$ and $t$ represent compression and tension, respectively.

   Plastic work $W_p^{*}$ in above limiting stress is defined as:

   $$W_p^{*}=\frac{W_p}{W_p^{ref}}$$

   Where, $W_p^{ref}$ is unit reference plastic work per volume.

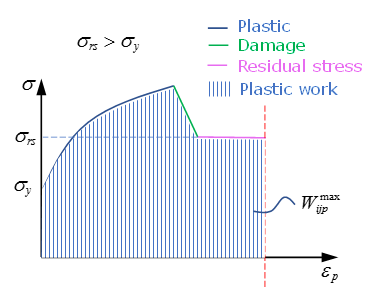
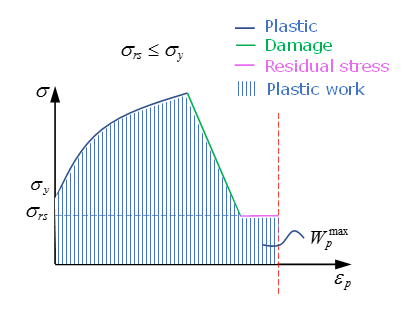
   This criterion represents a second order closed three-dimensional Tsai-Wu surface in ${\sigma }_1$ , ${\sigma }_2$ and ${\sigma }_{12}$ space. This surface is scaled, moved and rotated due to the variation of plastic work and true strain rate.

   Note: For shear, the parameters determining nonlinear behavior are the same in tension and compression.
4. Damage with tensile strain and energy failure.
   This material could describe in plane and out-of-plane damage.

   • In plane damage with damage factor $d_i$

     Global tensile strain damage between ${\epsilon }_{ti}$ and ${\epsilon }_{fi}$ controlled by the damage factor $d_i$ , which is given by:

     $d_i=\min \left(\frac{{\epsilon }_i-{\epsilon }_{ti}}{{\epsilon }_i}\cdot \frac{{\epsilon }_{mi}}{{\epsilon }_{mi}-{\epsilon }_{ti}},d_{\max }\right)$ in directions, $i$ = 1, 2

   • E-modulus

     E-modulus is reduced according to damage parameter if, ${\epsilon }_{ti}\le {\epsilon }_i\le {\epsilon }_{fi}$ :

     $$E_{ii}^{reduced}=E_{ii}(1-d_i)$$

     E-modulus is reduced according to damage parameter, if ${\epsilon }_i>{\epsilon }_{fi}$ :

     $$E_{ii}^{reduced}=E_{ii}(1-d_{\max })$$

     In this case, damage is set to $d_{\max }$ and it is not updated further.

   • Yield Stress
     Yield stress is reduced since below damage strain in different loading:

     • ${\epsilon }_i^{\text{t1}}$ and ${\epsilon }_i^{t2}$ in tension
     • ${\epsilon }_i^{\text{c1}}$ and ${\epsilon }_i^{c2}$ in compression
     • ${\epsilon }_{12}^{\text{1}}$ and ${\epsilon }_{12}^2$ in shear
     For example, tensile in direction 1 will be reduced when ${\sigma }_{1\max }^t$ at ${\epsilon }_i^{\text{t1}}$ and until residual stress 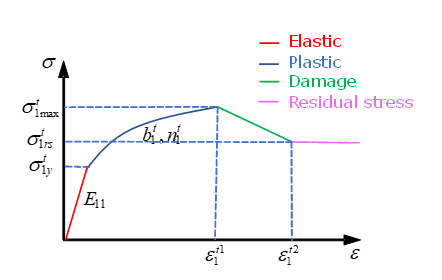${\sigma }_{1rs}^t$ at ${\epsilon }_1^{t2}$ .

     
     
     

   • Element deletion is controlled by the I_off flag.

   Out-of-plane damage (delamination) with $\gamma$ .

   The simplest delamination criterion is based on the evaluation of out-of-plane shear strains ( ${\gamma }_{31}$ and ${\gamma }_{23}$ ) with $\gamma =\sqrt{{({\gamma }_{13})}^2+{({\gamma }_{23})}^2}$ .

   • Element stresses and are gradually reduced if, ${\gamma }_{\max }>\gamma >{\gamma }_{ini}$
   • The element is completely removed (fails), if $\frac{\gamma -{\gamma }_{ini}}{{\gamma }_{\max }-{\gamma }_{ini}}>d_{3\max }$ in one of the shell layers.
5. Element rupture with strain, damage and energy failure criterion.
   • Element rupture (stress set to zero) depends on the option WP_fail where either the global maximum plastic work $W_p^{\max }$ or directional maximum plastic work $W_{ijp}^{\max }$ will be taken into account. When the stress value of all layers is zero, the element is deleted.

     If WP_fail=0

     If the residual stress is greater than yield stress ( ${\sigma }_{rs}>{\sigma }_y$ ), then the element layer ruptures (stress set to zero) if it reaches the directional maximum plastic work $W_{ijp}^{\max }$ . Example, tensile loading in direction 1 with ${\sigma }_{1rs}^t>{\sigma }_{1y}^t$ , element layer ruptured if plastic work reach ${{\displaystyle {\text{W}}_{\text{1}p}^{\max }}}^t$ .

     
     
     

     If the residual stress is not greater than yield stress ( ${\sigma }_{rs}\le {\sigma }_y$ ), then the element layer ruptures if it reaches the global maximum plastic work $W_p^{\max }$ . Example, tensile loading in direction 2 with ${\sigma }_{2rs}^t\le {\sigma }_{2y}^t$ , element layer ruptured if plastic work reach $W_p^{\max }$ .

     
     
     

     If WP_fail=1

     The element layer ruptures when it reaches the directional maximum plastic work in its direction $W_{ijp}^{\max }$ even if the residual stress is less than the yield stress.

   • Element deletion is controlled by the option I_off which uses the following criteria or combinations of criteria.
     • Element rupture could be due to reaching the strain criterion ( ${\epsilon }_i>\begin{array}{c}{\epsilon }_{\mathrm{m}i}\end{array}$ in direction $i$ )
     • Damage criterion ( $d_i>\begin{array}{c}{d}_{\max }\end{array}$ in direction $i$ )
     • Plastic work failure criterion
     Note:

     • When using the plastic work failure criterion WP_fail, if a directional maximum plastic work is not entered, then the global maximum plastic strain will be taken.
     • Similarly, when ICC_global=4, the global maximum plastic work or directional maximum plastic work will be scaled based on strain rate.

       For example, with a tensile loading in direction 2, the maximum plastic work values are scaled:

       $$W_p^{\max }\cdot \left(1+c\ln \frac{{\dot{\epsilon }}_2}{{\dot{\epsilon }}_0}\right)$$

       and

       $$W_{2p}^{{\max }^t}\cdot \left(1+c_2^t\ln \frac{{\dot{\epsilon }}_2}{{\dot{\epsilon }}_0}\right)$$

6. The Ratio field can be used to provide stability to composite shell components. For example, it allows you to delete unstable elements wherein, all but one layer has failed. This last layer may cause instability during simulation due to a low stiffness value. This option is available for strain and plastic energy based brittle failure.
7. Tensile strain and energy failure criterion of LAW25 is not available for orthotropic shells with /PROP/TYPE9.
8. The unit of $W_p^{ref}$ is energy per unit of volume. If set $W_p^{ref}$ as default value (0) is encountered, the default value is 1 unit of the model.
   Example:

   • If unit system of kg-m-s used in model, then $W_p^{ref}=1\left[\frac{J}{m^3}\right]$
   • If unit system of Ton-mm-s used in model, then $W_p^{ref}=1\left[\frac{mJ}{m{m}^3}\right]$
   For proper conversion of this value if changing units in pre- and post-processor, it is advised to replace the default value by the true value “1”, so that the value of $W_p^{ref}$ will be automatically converted. Leaving the $W_p^{ref}$ field to “0” may result in errors in case of automatic conversion.

   Note: A local unit system can be created for the material to avoid conversion.
9. Output for post-processing:
   • To post-process this material in the animation file, the following Engine cards should be used:
     • /ANIM/SHELL/WPLA/ALL for plastic work output
     • /ANIM/BRICK/WPLA for plastic work output
     • /ANIM/SHELL/TENS/STRAIN for strain tensor output in the elemental coordinate system
     • /ANIM/SHELL/TENS/STRESS for stress tensor output in the elemental coordinate system
     • /ANIM/SHELL/PHI angle between elemental and first material direction
     • /ANIM/SHELL/FAIL number of failed layers.
   • To post-process this material in the time-history file, the following definitions in /TH/SHEL or /TH/SH3N card should be used:
     • PLAS (or EMIN and EMAX) for minimum and maximum plastic work in the shell.
     • WPLAYJJ (JJ=0 to 99) for plastic work in a corresponding layer.
   • The output file (*0001.out) displays some information when the failure criteria is met:
     • Failure 1 and 2 means tensile failure direction 1 or 2, respectively
     • Failure -P means global plastic work failure
     • P-T1 / P-T2 means plastic work failure in tension direction 1 or 2, respectively
     • P-C1 / P-C2 means plastic work failure in compression direction 1 or 2, respectively
     • P-T12 means plastic work failure in shear

     The failure message also indicates which element and which layer is affected. It is output when the failure criteria is met for an integration point. As Batoz elements have 4 integrations points for each layer, this message may be output up to 4 times per layer and elements in this case.

10. /VISC/PRONY can be used with this material law to include viscous effects.
11. The different modes of failure can be output using /H3D/ELEM/DAMG/ID=Mat_ID with the keyword MODE (= I or ALL). The correspondence between the modes and the damage variables are:
    • Mode 1: Tensile damage in direction 1
      $$d_1=\min \left(\frac{{\epsilon }_1-{\epsilon }_{t1}}{{\epsilon }_1}\cdot \frac{{\epsilon }_{m1}}{{\epsilon }_{m1}-{\epsilon }_{t1}},d_{\max }\right)$$
    • Mode 2: Tensile damage in direction 2
      $$d_2=\min \left(\frac{{\epsilon }_2-{\epsilon }_{t2}}{{\epsilon }_2}\cdot \frac{{\epsilon }_{m2}}{{\epsilon }_{m2}-{\epsilon }_{t2}},d_{\max }\right)$$
    • Mode 3: Global maximum plastic work
      $$d_3=\min \left(\frac{W_p}{W_p^{\max }},\text{ 1}\right)$$
    • Mode 4: Failure index for yield stress in direction 1
      For this mode, the failure index $d_4$ takes its value between -2 and 2

      • From 0 to 1: working phase in tension, and from 0 to -1: working phase in compression (in green)
      • From 1 to 1.95: damage phase in tension, and from -1 to -1.95: damage phase in compression (in yellow)
      • At 2.0: element deletion in tension and at -2 element deletion in compression (in red)

        

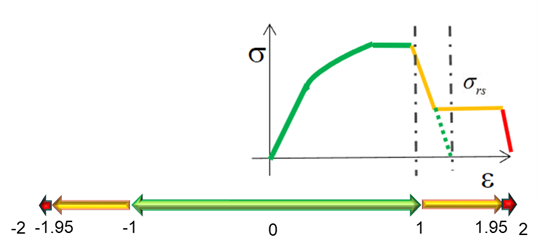
    • Mode 5: Failure index for yield stress in direction 2

      Same as Mode 4 but in direction 2. It is denoted as $d_5$

    • Mode 6: Failure index for yield stress in shear plane 12

      Same as Mode 4 and 5 but in shear plane 12. For this mode, negative values are not encountered as the sign is not considered for the shear stress. It is denoted as $d_6$ .

12. A global failure index can be plotted using /H3D/ELEM/DAMG/(ID=Mat_ID) without MODE option. It corresponds to:

    $\begin{array}{l}{d}_{GLOB}=\max \left(d_1,d_2,d_3,\left|d_4\right|-1,\left|d_5\right|-1,d_6-1\right)\\ \text{if }1<\left|d_4\right|\le 2\text{, }1<\left|d_5\right|\le 2\text{, }1<d_6\le 2\end{array}$