Seam Weld Fatigue Analysis

Seam Weld Fatigue analysis is available to facilitate Fatigue analysis for seam welded structures. It allows you to simulate the Fatigue failure at the seam weld joints to assess the corresponding fatigue failure characteristics like Damage and Life.

The Volvo method implemented in HyperLife is based on a research paper Fatigue Life Prediction of MAG-Welded Thin-Sheet Structures published by M. Fermér, M Andréasson, and B Frodin. The method is a hot spot stress approach applicable to thin metal sheets. Hot spot stress is calculated from grid point forces at weld line. The method showed a good agreement with laboratory test results for sheet thickness between 1.0 mm and 3.0 mm. The method typically requires two SN curves. One is a bending SN curve which is dominated by bending stress, and the other is a membrane SN curve which dominated by membrane stress.

Implementation

Modeling Requirements

With the Volvo method, the Seam Weld Fatigue Analysis implementation in HyperLife consists of the following modeling requirements.

Weld sections to be analyzed for seam weld fatigue should be meshed with CQUAD4 elements whenever possible. CTRIA3 elements may be used for corner weld if inevitable and for closing the end of weld line, if necessary. Other element types are currently not supported for seam weld fatigue.
The weld should be modeled by a single or double row of CQUAD4 elements. If a 2 sided fillet is to be modeled, a third row of CQUAD4 may be used.
The thickness of the weld element is the same as the effective throat.
The mesh size around the weld should be as regular as possible. Although this method is less sensitive to mesh size, a mesh size of about 10 mm would be a good choice according to Fermér, Andréasson, Frodin. This paper showed that large hot spot stress differences did not exist between mesh size 12 mm and mesh size 5 mm in case of a regular mesh.
The weld element can be referenced through Sets/Parts. Custom Zones assist in creating user-defined sets in HyperLife.
The weld element normal direction should point outwards such that the normal direction is toward the weld toe, not toward the weld root. The normal direction of weld element plays a critical role in determining the weld toe and the surface to be examined on the base of the weld.

Weld Basics

A weld can be used to join two parts together. Welds vary in shapes and sizes depending on the type of joint that is required. For example, welds for fillets and overlap joints are different. Typically, a weld consists of the following parts:

Face
Toes
Throat
Root
Legs

The face of a weld is the outer surface of the weld that is visible to you. The toes are the points where the base material of the connected plates intersects with the weld material along the weld face. The weld throat is the distance between the root and the center of the face. The weld root is point of deepest weld penetration and it is opposite to the weld face. The weld legs extend from the root of the weld to the toes.

Good Weld Design Practice

This section provides a basic overview of stress concentrations in welded structures and a few recommendations for good weld design. This section should not be considered as a complete weld design guide and does not cover an exhaustive list of weld design recommendations.

All welds contain stress concentrations which will reduce the fatigue life. A local stress concentration occurs at the toe of the weld and is controlled by the welding process conditions. This stress concentration is embedded in a macroscopic stress concentration that is a result of the design of the weld joint.

Weld shape-based stress concentration:
Figure 2 shows the stress concentration at the toe of a weld. Its magnitude depends on the flank angle, $θ$ , local weld toe radius, r, and plate thickness, t. The concept of a weld reinforcement is a misnomer as you can see that the stress concentration actually increases with increasing weld metal, that is, an increase in flank angle, $θ$ .
Figure 2. Stress Concentration versus Weld Radius and Plate Thickness for Seam Weld Fatigue
Weld design-based stress concentration:
The second stress concentration comes from the joint design. Stress concentrations arise whenever there is a change in stiffness in the structure. It can result from either an increase of decrease in stiffness. For example, a hole in a plate will have about the same stress concentration as a rigid boss added to the plate. Here are some examples of weld joints contrasting good and poor design practice.
First you need to consider a cover plate welded to a bending beam. A large stress concentration exists at the end of the cover plate because of the large change in stiffness. A better design is shown on the right side where there is a more gradual change in stiffness.
Figure 3. (a) Incorrect Weld Design; (b) Correct Weld Design: Gradual Stiffness Gradient

A second source of stress concentration is unintentional bending stresses caused by asymmetric geometries. The design on the left will have larger bending stresses than the double lap joint on the right side.
Figure 4. (a) Incorrect Weld Design; (b) Correct Weld Design: Double Lap Joint Symmetric Geometry

Welding plates of differing thicknesses or widths is always problematic. Just as above, the easiest geometry to weld has the largest stress concentration. You should always consider moving the welds to lower stress areas in the structure and have a gradual transition in stiffness such as the joint shown Figure 5(b).
Figure 5. (a) Incorrect Weld Design; (b) Correct Weld Design: Gradual Stiffness Transition

Supported Weld Types

HyperLife supports certain types of welds for Seam Weld Fatigue Analysis.

The type can be selected using the Weld Type field in the Assign Material dialog once the weld set/part is selected.

Only one row of elements can be defined for the weld face elements or either of the weld legs.
The damage calculation locations are automatically chosen based on the weld type (as explained in Fillet). With the exception of the throat damage location, both the root and toe damage locations are evaluated based on the grid point forces and subsequent stresses induced in the corresponding elements adjacent to the weld elements. For throat damage, the weld element grid point forces, and subsequent stresses are directly considered.
HyperLife currently supports the following weld types.

Fillet

A fillet weld is a weld joining two sheets at an angle. Typical failure locations are marked in Figure 6(a). A fillet weld may be modeled by inclined CQUAD4 as in Figure 6(b). Depending on how much the weld penetrates, the weld may be modeled by a single or double row of CQUAD4. If a Two-sided fillet is to be modeled, three rows of CQUAD4 may be used.

HyperLife evaluates failures at root and toe when a weld element is CQUAD4. If CTRIA3 is used for a weld element, only toe is evaluated.

T-joint

One-sided One Row
For a One-sided One Row T-joint, the weld element normal direction should point towards the weld toe. The nodes of the weld element are in line with the weld toes. The length should be determined by the actual dimensions of the weld element (typically L=T₁+T₂).
Figure 7. Representation of a One-sided T-Joint Fillet Weld with One Row of CQUAD4 Elements

The thickness of the weld element is the effective weld throat (typically it is equal to L/1.414).
One-sided Two Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 8, the weld has penetrated more than the weld in Figure 7. For a One-sided Two Row T-joint, the two weld element normal directions should point towards the weld toe. The length should be determined by the actual dimensions of the weld element (typically L=T₁+T₂).
Figure 8. Representation of a One-Sided T-Joint Fillet Weld with Two Rows of CQUAD4 Elements

The thickness of the weld element is recommended to be set equal to 0.35*L.
Two-sided Two Row
For a Two-sided Two Row T-joint, the weld element normal directions should point towards the corresponding weld toe. The nodes of the weld elements are in line with the corresponding weld toes. The length should be determined by the actual dimensions of the weld element (typically L=T₁+T₂).
Figure 9. Representation of Two-Sided T-Joint Fillet Weld with Two Rows of CQUAD4 Elements

The thickness of the weld element is the effective individual weld throat (typically it is equal to 1.414*L).
Two-sided Three Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 10, the welds have penetrated more than the welds in Figure 9. For a Two-sided Three Row T-joint, the two weld element normal directions should point towards the corresponding weld toe. The weld element normal for the central vertical element can point to either weld toe.
Figure 10. Representation of a Two-sided T-Joint Fillet Weld with Three Rows of CQUAD4 Elements

Cross-joint

For a cross-joint, all weld elements associated with one cross joint weld should be specified in a single part/set, otherwise HyperLife will treat the cross-joint fillet weld as separate multiple welds and may output unexpected results. Additional requirement for a cross-joint is that the joint should be symmetric.

One-sided One Row
For a One-sided One Row Cross-joint, the weld element normal direction should point towards the corresponding weld toe.
Figure 11. Representation of a One-sided Cross-Joint Fillet Weld with One Row of CQUAD4 Elements Each
One-sided Two Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 12, the welds have penetrated more than the welds in Figure 11. For a One-sided Two Row Cross-joint, the weld element normal direction should point towards the corresponding weld toe. The vertical weld element normals should also point towards the corresponding weld toe.
Figure 12. Representation of a One-sided Cross-Joint Fillet Weld with Two rows of CQUAD4 Elements Each
Two-sided Two Row
For a Two-sided Two Row Cross-Joint, the weld element normal direction should point towards the corresponding weld toe.
Figure 13. Representation of a Two-sided Cross-Joint Fillet Weld with Two Rows of CQUAD4 Elements Each
Two-sided Three Row
Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. In Figure 14, the welds have penetrated more than the welds in Figure 12.
For a Two-sided Three Row Cross-Joint, the weld element normal direction should point towards the corresponding weld toe. The normals of the vertical weld elements can point towards either weld toe on each side.
Figure 14. Representation of a Two-sided Cross-Joint Fillet Weld with Three Rows of CQUAD4 Elements Each

Overlap or Laser Edge Overlap

An overlap weld is a weld joining two overlapped sheets in parallel. Figure 15 shows possible failure locations. HyperLife evaluates these locations. Typical failure locations are marked in Figure 15. An overlap weld may be modeled by inclined and vertical CQUAD4. Depending on how much the weld penetrates, the weld may be modeled by a single or double row of CQUAD4.

Meshing rules are the same as that for fillet weld. Normal direction of weld element should be toward weld toe. Weld nodes should be along the line of the weld toe. Weld element thickness should be effective weld throat. In laser weld, failure at weld throat is evaluated as well as weld toe and weld root.

Two Row Overlap

Multiple rows are recommended for welds where the weld penetration is high and the weld typically forms the basis for contact between the two plates. Such welds are more rigid compared to welds where the penetration is lower, thereby additional rows of weld shell elements are required to capture the behavior. The typical length of the weld element is L=T₁+T₂.

Typical weld element thickness is about 0.27*L.

Figure 16. Representation of a Two Row Overlap Weld

One Row Overlap or One Row Laser Edge Overlap

For overlap, weld element thickness should be 2 times the thickness of the thinner sheet. Its minimum thickness is 3mm. For laser edge overlap, weld element thickness should be effective weld throat. It is about 0.7* the upper sheet thickness.

Figure 17. Representation of a One Row Overlap Weld or Laser Edge Overlap Weld

One Row Overlap or One Row Laser Edge Overlap (Alternative)

The previous weld can also be modeled as shown in Figure 18.

Figure 18. Representation of an Alternative Approach for a One Row Overlap or Laser Edge Overlap

Laser Overlap

The thickness of the weld element should be the weld width. The weld width should be 90% of the thickness of the thinner sheet. Its minimum thickness is 1 mm. The laser overlap welds are intended for very thin sheets (> 1 mm).

Failure Evaluation

Failure evaluation points differ from one weld type to another.

The following sections provide information about which locations of the weld elements are used for failure evaluation in Seam Weld Fatigue Analysis. Figure 20 shows how the identification points are illustrated in subsequent images.

Figure 20. Attributes for Proper Identification of Entities

Fillet

The weld toe and root locations are evaluated. Throat location is not evaluated.

Note: The arrows in Figure 21 and Figure 22 indicate surfaces for evaluation (surface of the shell elements adjacent to the weld element).

Figure 21. Failure Locations for One Row Fillet

Figure 22. Failure Locations for Two Row Fillet

Hot Spot Stress

HyperLife calculates hot spot stress based on grid point force of a toe/root element.

In the original approach suggested by Fermér, Andréasson, Frodin, grid point forces contributed to the element of interest were directly used without any "adjustment". Later research [P. Fransson and G. Pettersson, 2000] showed that averaging grid point forces made grid point forces less mesh sensitive.

The calculation method implemented in HyperLife includes weighted averaging of grid point forces, as:

HyperLife identifies potential damage locations at weld toe, weld root, weld throat and their evaluation surface from weld elements location and its normal direction (as shown in previous sections).
For the corresponding root and toe damage locations (in adjacent elements), and in the throat (in the weld element), local coordinate systems are constructed. The local X axis is constructed in the direction perpendicular to and away from the corresponding weld element face at the center of the adjacent element on the weld line (the X axis is in located in the plane of the adjacent element). The local Y axis is constructed perpendicular to this X axis in the plane of the adjacent element.
Figure 23. Seam Weld Stress Calculation Example
Grid point forces are calculated at grids (Q and R) of the adjacent element (2) along the weld line. Grid point force contributions are sourced from elements attached (1 and 3) to the adjacent element.
Grid point forces are calculated as:
$f_{Q} = f_{Q 1} + f_{Q 2}$
$f_{R} = f_{R 2} + f_{R 3}$
Moments are written as:
$m_{Q} = m_{Q 1} + m_{Q 2}$
$m_{R} = m_{R 2} + m_{R 3}$
At each node ( $Q$ and $R$ ) of the adjacent element that lies on the weld line, averaged grid point forces/moments weighted by length of the adjacent element and the attached element on the weld toe line are calculated.
Weighted forces are written as:
$f_{Q}^{R I G H T} = \frac{L_{2}}{L_{1} + L_{2}} f_{Q}$
$f_{R}^{L E F T} = \frac{L_{2}}{L_{2} + L_{3}} f_{R}$
Weighted moments are written as:
$m_{Q}^{R I G H T} = \frac{L_{2}}{L_{1} + L_{2}} m_{Q}$
$m_{R}^{L E F T} = \frac{L_{2}}{L_{2} + L_{3}} m_{R}$
Line Forces and Moments are calculated based on the weighted grid point forces and moments. These line forces and moments from both ends of the adjacent element on the weld line are averaged to generate the line force and moment at the midpoint ( $L$ ).
Line Forces are calculated as:
$f_{L Q}^{R I G H T} = \frac{2}{L_{2}} (2 f_{Q}^{R I G H T} - f_{R}^{L E F T})$
$f_{L R}^{L E F T} = \frac{2}{L_{2}} (2 f_{R}^{L E F T} - f_{Q}^{R I G H T})$
Line Moments are calculated as:
$m_{L Q}^{R I G H T} = \frac{2}{L_{2}} (2 m_{Q}^{R I G H T} - m_{R}^{L E F T})$
$m_{L R}^{L E F T} = \frac{2}{L_{2}} (2 m_{R}^{L E F T} - m_{Q}^{R I G H T})$
The averaged line forces and moments at the midpoint, $L$ , for element 2 are:
$f_{2} = \frac{f_{L Q}^{R I G H T} + f_{L R}^{L E F T}}{2}$
$m_{2} = \frac{m_{L Q}^{R I G H T} + m_{L R}^{L E F T}}{2}$
The line force and moment at the midpoint are then resolved in the local coordinate system constructed in step 2 to generate $f_{2 X}$ and $m_{2 Y}$ respectively. This force and moment pair leads to tensile and bending stresses in the adjacent element with respect to the weld line. These are the forces that are used to calculate stresses.
Stresses are then calculated normal to the weld line for the adjacent element from this force moment pair. Stresses are calculated for both top and bottom of the shell element, and depending on the type of weld, either one or both are used for fatigue calculations. This is the final hot spot stress used in further S-N Fatigue Damage Evaluation. For addition information, refer to Stress-Life (S-N) Approach.
$σ_{T O P} = \frac{f_{2 X}}{T} + 6 \frac{m_{2 Y}}{T^{2}}$
$σ_{B O T T O M} = \frac{f_{2 X}}{T} - 6 \frac{m_{2 Y}}{T^{2}}$

Fatigue Properties

There are a few fatigue properties relevant to Seam Weld Fatigue Analysis that allow you to control the fatigue behavior.

Bending Ratio

Experiments show that two types of SN curves are required to perform Seam Weld Fatigue Analysis based on a method suggested by M. Fermér, M Andréasson, and B Frodin. Based on lab tests, two SN curves were plotted (Figure 24). The upper curve is obtained in tests where the maximum stress is dominated by Bending Moment (

m_{2 Y}

) and the lower curve is obtained from tests where membrane force (

f_{2 X}

) dominates the maximum stress.

Figure 24. Example Stress Amplitude versus Fatigue Life log(N) for Bending dominated versus Membrane Dominated Structure

The upper and lower curves are referred to as Bending SN curve and Membrane SN curve, respectively. It is recommended that membrane SN curve should be used when membrane stress dominates in an element, and bending SN curve should be used when bending stress dominates. Interpolation between the two curves may be carried out depending on the degree of bending dominance.

Degree of bending dominance can be determined by the average bending ratio ( $r_{B}^{A V G}$ ). First, the bending ratio ( $r$ ) is defined as:

r = \frac{| σ_{B} |}{| σ_{B} | + | σ_{M} |}

Where,

$σ_{B}$: Maximum bending stress equal to $6 \frac{m_{2 Y}}{T^{2}}$
$σ_{M}$: Maximum membrane stress equal to $\frac{f_{2 X}}{T}$

The average bending ratio ( $r_{B}^{A V G}$ ) for an element is defined as:

r_{B}^{A V G} = \frac{\sum_{i = 1}^{n} (r_{i} {[σ_{T O P}^{2}]}_{i})}{\sum_{i = 1}^{n} {[σ_{T O P}^{2}]}_{i}}

Where,

${[σ_{T O P}^{2}]}_{i}$: Square of the maximum stress at the top surface of shell element $i$ at which the damage is calculated (that is, root, toe, or throat shell elements)
$r_{i}$: Bending ratio of shell element $i$ .

is the

An interpolation factor ( $I F$ ) is now defined as:

$I F = 0.0$ when $0.0 \leq r_{B}^{A V G} \leq r_{B}^{C R I T}$

$I F = \frac{r_{B}^{A V G} - r_{B}^{C R I T}}{1 - r_{B}^{C R I T}}$ when $r_{B}^{C R I T} < r_{B}^{A V G} \leq 1.0$

The $r_{B}^{C R I T}$ value is defined by the BRATIO field in the Assign Material dialog. It is set to 0.5 by default. If average bending ratio ( $r_{B}^{A V G}$ ) is less than or equal to the critical bending ratio ( $r_{B}^{C R I T}$ ), then the Membrane SN curve is used to assess damage. If average bending ratio is greater than the critical bending ratio, then an SN curve that is interpolated between membrane SN curve and the bending SN curve is used. The value of the interpolation factor ( $I F$ ) is used in the linear interpolation method as illustrated in Figure 25. For example, if you consider the Fatigue Strength coefficient value (SR1_i) for the interpolated curve, the calculation is performed as:

S R 1_i = [S R 1_m + (S R 1_b - S R 1_m) I F]

Figure 25. Example Stress Amplitude versus Fatigue Life log(N) for Bending dominated versus Membrane Dominated structure

Thickness Correction

The thickness correction process is for size effect correction. SN curves are based on test results from a particular size of the specimen. In reality, the stress versus life curve may vary depending on specimen size. Therefore, thickness correction parameters can be used to correct for this effect. It may be applied based on the thickness $T$ of each shell element under consideration for Fatigue calculation (that is, toe, root, or throat element). The calculations are:

If $T \leq T R E F$ , then there is no Thickness Correction.

If $T > T R E F$ , HyperLife increases stress based on HyperLife:

σ_{T O P / B O T T O M} = σ_{T O P / B O T T O M} {(\frac{T}{T R E F})}^{T R E F_N}

This results in fatigue life reduction, making the design more conservative. TREF and TREF_N can be defined via the corresponding fields in the Assign Material dialog. The default values are 25 and 0.2 respectively. The defaults are in mm.

Thickness Correction can be turned on or off using the corresponding Thickness Correction field in the Fatigue Module dialog for Seam Weld Fatigue Analysis.

Mean Stress Correction

FKM mean stress correction is supported for Seam Weld Fatigue. Stress sensitivity can be defined in the Fatigue Module dialog via the FKMMSS field. Mean stress correction for Seam Weld fatigue can be enabled through the Seam Weld Fatigue Module dialog.

For more information on FKM mean stress correction, see the FKM section under Uniaxial S-N Fatigue.

Input/Output

To activate Seam Weld Fatigue Analysis, the Welds icon from the Fatigue Modules should be selected.

Fatigue Elements

Currently, shell elements (preferably CQUAD4) are supported for the seam weld calculations

Fatigue Parameters

The Method, FE Model Units, Mean Stress Correction, Certainty of Survival, and Thickness Correction are defined though the Seam Weld Fatigue dialog.

For more information on FKM mean stress correction, see the FKM section under Uniaxial S-N Fatigue.

Fatigue Material

The Material tool assists in assigning material properties to parts/sets and defining the SN curve.
User-defined materials can be created or selected from the SN material database.
Figure 28.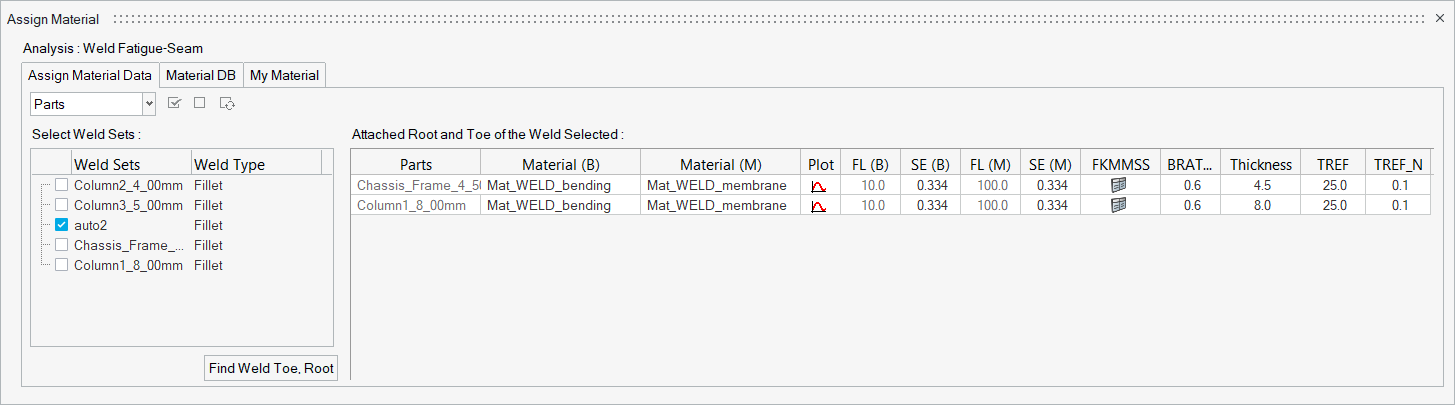

BRATIO: Critical bending ratio; Default = 0.5 (Real > 0.0)
TREF: Reference thickness for thickness effect consideration; Default = 25.0 (Real > 0.0)
TREF_N: Exponent for the thickness effect consideration; Default = 0.2 (Real ≥ 0.0)

Fatigue Loads

Load histories (channels) can be imported, or Block sequence loading can be created.
Events define the pairing of FEA subcases and load histories.

Output

Output for Seam Weld Fatigue Analysis is provided similar to regular fatigue analysis results.

seamweld_fig29 — Figure 29. Example Cross Joint Fillet Weld Output for Damage

seamweld_fig30 — Figure 30. Example Cross Joint Fillet Weld Output for Toe/Root/Throat elements