HS-1705： 簡単なフィットスタディ

空間充填のDOEスタディをセットアップし、続いてフィットスタディをセットアップする方法について学習します。

開始に先がけ、HS-1700: 簡単なDOEスタディを完了するか、もしくは<hst.zip>/HS-1705/にあるHS-1700.hstxアーカイブファイルをインポートします。
ベース入力テンプレートは、それぞれX、Yとラベル付けされた2つの入力変数DV1、DV2を定義します。スタディの目的は、2つの関数X+Yおよび1/X + 1/Y – 2を成す2つの入力変数X、Yについて調査することです。

DOEの実行

  1. DOEを追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
      Add（追加）ダイアログが開きます。
    2. Select Type（タイプの選択）からDOEを選択します。
    3. Definition from（定義元）に、アプローチを選択します。
    4. Setup（セットアップ）を選択し、OKをクリックします。
  2. スタディ仕様を定義します。
    1. DOE 2 > Specifications（スタディ仕様）ステップに進みます。
    2. ワークエリア内でモードをHammersleyにセットします。
    3. Apply（適用）をクリックします。
  3. タスクを評価します。
    1. DOE 2 > Evaluate（評価）ステップに進みます。
    2. Evaluate Tasks（計算実行）をクリックします。
      評価の結果が、ワークエリア内に表示されます。
  4. DOE 2 > Post Processing（ポスト処理）ステップに進みます。
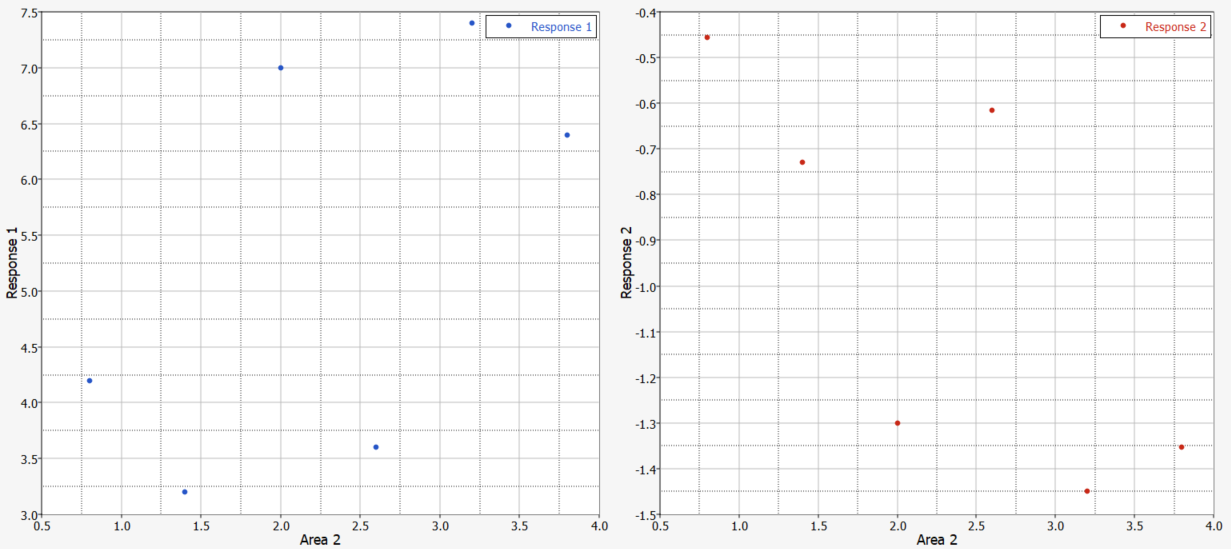
  5. Area 2とResponse 1、Response 2の間の依存を示したプロットを確認します。
    1. Scatter（散布図）タブをクリックします。
    2. Channel（チャンネル）セレクターを使って、X AxisをArea 2に、Y AxisをResponse 1とResponse 2の両方にセットします。
    3. 散布図を比較し、設計空間を通して一様に分布しているかどうかを確認します。
      図 1.


フィットスタディの実行

  1. Fit（フィット）を追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
    2. Add（追加）ダイアログで、Fit Existing DataFit（既存データフィット）とSetup（セットアップ）を選択し、OKをクリックします。
  2. スタディ仕様を定義します。
    1. Specifications（スタディ仕様）タブをクリックします。
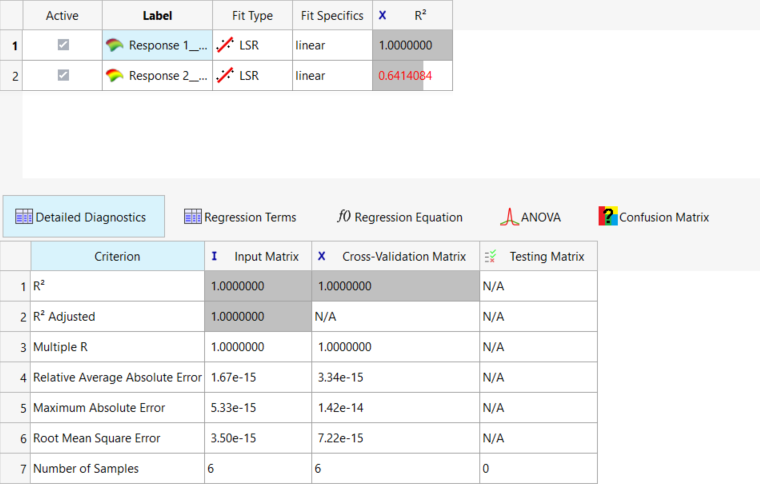
    2. ワークエリアのFit Type（近似手法）列で、両方の出力応答にLeast Squares Regression（最小二乗法） (LSR)を選択します。
    3. Apply（適用）をクリックします。
    図 2.


  3. マトリックスを定義します。
    1. Fit 1 > Specifications（スタディ仕様）ステップに進みます。
    2. ワークエリアで、Origin（原点）をApproach（アプローチ）に設定します。
    3. Origin Settings（原点設定）に、DOE 2を選択します。
    4. 適用をクリックします。
    図 3.


  4. タスクを評価します。
    1. Fit 1 > Evaluate（評価）ステップに進みます。
    2. Evaluate Tasks（計算実行）をクリックします。
  5. 結果をポスト処理します。
    1. Fit 1 > Post Processing（ポスト処理）ステップに進みます。
    2. Residuals（残差）タブをクリックし、両方の出力応答の残差を確認します。

      一覧内のデータは、構築されたフィットからの予測値と実際の値との差を示しています。Response_1の 誤差（％）が6つのランすべてについて0.0であり、Response_2の誤差（％）は35%までです。Response_1のLSRフィッティングは許容可能ですが、Response_2のLSRフィッティングはかなり大きくなっています。

    3. Diagnostics（診断）タブをクリックし、フィットの全体的な品質を確認します。

      フィットの相対的な品質を示す数値がいくつか表示されます。決定係数の値は、フィットによって説明されえるデータ内の分散のパーセンテージとして解釈できます。

      Response_1については、フィットはデータ分散の100%を捕捉しています。Response_1は実際線形関数であし、1次回帰は誤差なしで実際のデータと一致するため、これは理に適っています。Response_2については、フィットが分散の約90%を説明していることが示されています。
      図 4.


  6. Specifications（スタディ仕様）ステップに戻り、出力応答の応答について許容可能なフィッティングを見出すまで別の手法を試してください。
    1次の最小自乗では、データの分散のほとんどを説明するフィットを得ますが、これは比較的大きい予測誤差を有します。