Internal Forces Computation

Nodes are numbered from 1 to $n$ , and strands are numbered from 1 to n-1 (strand $k$ goes from node N_k to node N_k+1).

Averaged Force

The averaged force in the multistrand is computed as:

Linear spring $F = \frac{K}{L^{0}} δ + \frac{C}{L^{0}} \dot{δ}$

Nonlinear spring $F = f (ε) \cdot g (\dot{ε}) + \frac{C}{L^{0}} \dot{δ}$

or, if

g

function identifier is 0:

図 2.

F = f (ε) + \frac{C}{L^{0}} \dot{δ}

or, if

f

function identifier is 0:

図 3.

F = g (\dot{ε}) + \frac{C}{L^{0}} \dot{δ}

Where, $ε$ is engineering strain $ε = \frac{L - L^{0}}{L^{0}}$ .

Where, $L^{0}$ is the reference length of element.

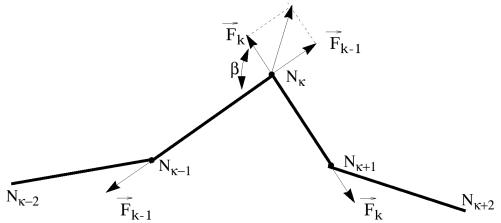
Force Into Each Strand

The force into each strand $k$ is computed as:

$F_{k} = F + Δ F_{k}$

Where,

Δ F_{k}

is computed an incremental way:

図 4.

Δ F_{k} (t) = Δ F_{k} (t - 1) + \frac{K}{l_{k}^{0}} δ ε_{k} - \frac{K}{L^{0}} δ ε

with $l_{k}^{0}$ the length of the unconstrained strand $k$ , $δ ε = ε (t) - ε (t - 1)$ and $δ ε_{k} = δ t u_{k} \cdot (v_{k + 1} - v_{k})$ .

Where, $u_{k}$ is the unitary vector from node N_k to node N_k+1.

Assuming:

図 5.

\frac{l_{k}}{l_{k}^{0}} = \frac{L}{L^{0}}

Where, $l_{k}$ is the actual length of strand $k$ .

Therefore, 式 3 reduces to:

図 6.

Δ F_{k} (t) = Δ F_{k} (t - 1) + \frac{K}{l_{}^{0}} (δ ε_{k} \frac{L}{l_{k}} - δ ε)

Friction

Friction is expressed at the nodes: if

μ

is the friction coefficient at node

k

, the pulley friction at node N_k is expressed as:

図 7.

Δ F_{k} (t) = Δ F_{k} (t - 1) + \frac{K}{l_{k}^{0}} δ ε_{k} - \frac{K}{L^{0}} δ ε

When equation 式 6 is not satisfied, $| Δ F_{k - 1} - Δ F_{k} |$ is reset to $(2 F + Δ F_{k - 1} + Δ F_{k}) \tanh (\frac{β μ}{2})$ .

All the

Δ F_{k}

(k=1, n-1) are modified in order to satisfy all conditions upon

Δ F_{k - 1} - Δ F_{k}

(k=2, n-1), plus the following condition on the force integral along the multistrand element:

図 8.

\sum_{k = 1, n - 1} l_{k} (F + Δ F_{k}) = L F

This process could fail to satisfy 式 6 after the

Δ F_{k} (k = 1, n - 1)

modification, since no iteration is made. However, in such a case one would expect the friction condition to be satisfied after a few time steps.

注: Friction expressed upon strands (giving a friction coefficient

μ

along strand

k

) is related to pulley friction by adding a friction coefficient

μ / 2

upon each nodes N_k and N_k+1.

Time Step

Stability of a multistrand element is expressed as:

図 9.

Δ t \leq \frac{\sqrt{C_{k}^{2} + ρ l_{k} K_{k}} - C_{k}}{K_{k}}, \forall k

with

K_{k} = \frac{M a s s o f t h e m u l t i s t r a n d}{L^{0}}

and (assuming 式 4):

図 10.

K_{k} = \max (\frac{K}{l_{k}^{0}}, \frac{F}{l_{k} - l_{k}^{0}}) = \max (\frac{K L}{l_{k} L^{0}}, \frac{F L}{l_{k} (L - L^{0})})

図 11.

C_{k} = \frac{(f (ε) \frac{d g}{d \dot{ε}} (\dot{ε}) + C)}{l_{k}^{0}} = (f (ε) \frac{d g}{d ε} (\dot{ε}) + C) \frac{L}{l_{k} L^{0}}