RD-V: 0210 Yeoh Hyperelastic Material

A one element model in tension used as a test model and compare with analytical results.

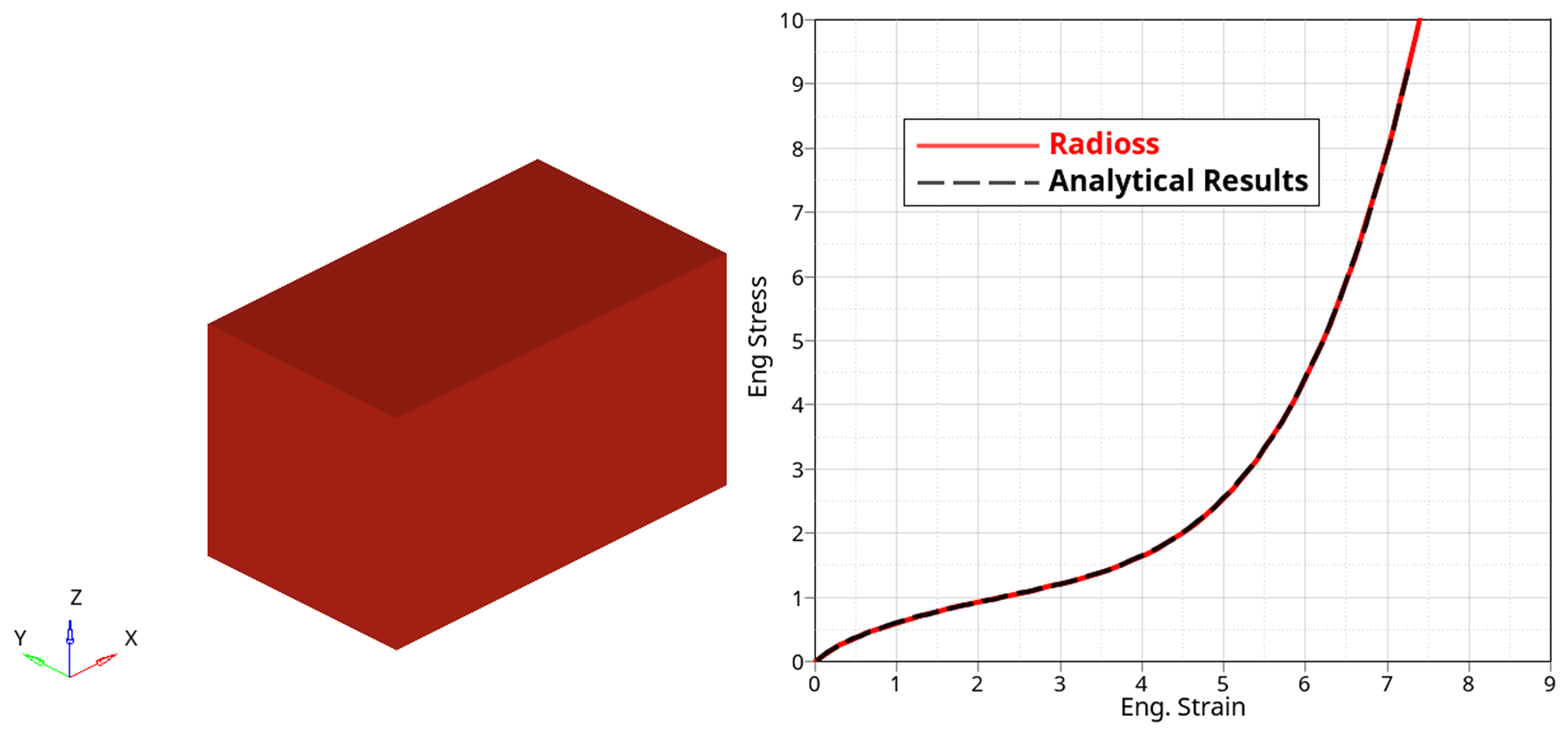
The Yeoh model can be used to describe nearly impressible hyperelastic materials, like rubber. Set Yeoh parameter with LAW94 and compare one element tension Radioss results with analytical results.

Options and Keywords Used

/MAT/LAW94 (YEOH)

Input Files

Before you begin, copy the file(s) used in this problem to your working directory.

RD-V-0210_Yeoh_Hyperelastic_Material.zip

Model Description

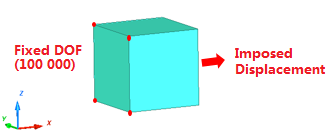
Uniaxial tensile one brick element with imposed displacement and fixed in other side only in X direction.

Units: mm, s, Mg, N, MPa

Properties: /PROP/SOLID with, I_solid=24, I_smstr=10, and I_cpre=1

Note: When using hyperelastic material laws, there are some recommended element property settings. When using solid elements, it is always better to mesh with 8 node /BRICK elements, if possible. If not, then /TETRA4 or /TETRA10 elements can be used. Recommended /PROP/SOLID for 8 nodes brick are, I_solid=10, I_cpre=1, with I_solid=24. If hourglassing occurs, then I_solid=18 can be used.

Simulation Iterations

Yeoh theory:
The Yeoh energy density is:
$W = \sum_{i = 1}^{3} [C_{i 0} {({\bar{I}}_{1} - 3)}^{i} + \frac{1}{D_{i}} {(J - 1)}^{2 i}]$
This example assumes an incompressible ( $J = 1$ ) hyperelastic material, then the strain energy density of Yeoh simplified, as:
$W = C_{10} {({\bar{I}}_{1} - 3)}^{1} + C_{20} {({\bar{I}}_{1} - 3)}^{2} + C_{30} {({\bar{I}}_{1} - 3)}^{3}$
With
${\bar{I}}_{1} = {\bar{λ}}_{1}^{2} + {\bar{λ}}_{2}^{2} + {\bar{λ}}_{3}^{2}$
Where,

${\bar{λ}}_{i}$

Deviatoric stretch with ${\bar{λ}}_{i} = J^{- \frac{1}{3}} λ_{i}$ and $λ_{i} = ε_{i} + 1$ .

$λ_{1}, λ_{2}, λ_{3}$

The stretch in principal direction 1, 2, 3.

$ε_{i}$

Engineer strain in principal direction I.

It shows only three parameters $C_{10}, C_{20}, C_{30}$ need to be defined for the (incompressible) Yeoh model.
Uniaxial test is used in this example, then:
$λ_{1} = λ$ and $λ_{2} = λ_{3} = λ^{- \frac{1}{2}}$
The Cauchy stress of Yeoh model is computed as:
$σ_{i} = \frac{λ_{1}}{J} \frac{\partial W}{\partial λ_{1}}$
In the uniaxial test, the Cauchy stress (true stress) in principal direction 1 is:
$σ_{1} = λ \frac{\partial W}{\partial {\bar{I}}_{1}} \frac{d {\bar{I}}_{1}}{d λ}$
The engineer stress is:
$σ_{1_e n g} = \frac{σ_{1}}{(ε_{1_e n g} + 1)}$
In this example, three material parameters are defined below:
$\begin{array}{l} C_{10} =0 .18 \\ C_{20} =-2e-3 \\ C_{30} = 5 e - 5 \end{array}$

Figure 3. Engineer stress-strain curve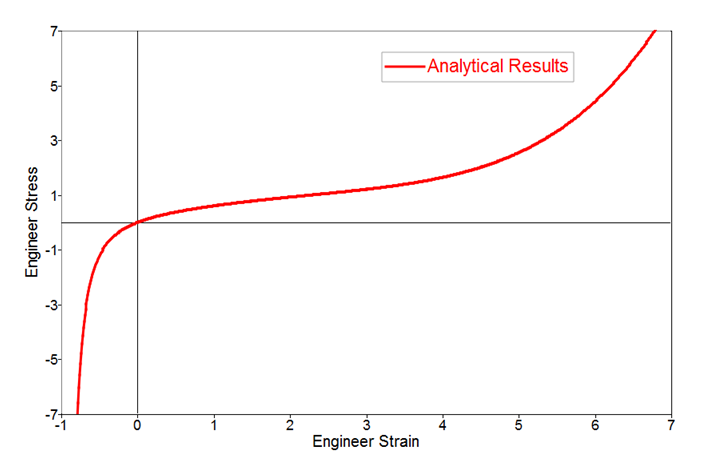
LAW94:
The hyperelastic model uses polynomial model and the Yeoh model is one of the polynomial model with only three parameters. In this example, viscous was not considered.

Results

In LAW94 Yeoh model, three parameters $C_{10}, C_{20}, C_{30}$ defined same as analytical case.

D1 needs to be defined in the material card. If D1 is not defined in LAW94, then the default Poisson’s ratio 0.495 is used.

Then 1/D1=17.94 is printed in the Starter output file.

This can be checked as follows:

$G = 2 C_{10} =2*0 .18=0 .36$

$D 1 = \frac{3 (1 - 2 ν)}{G (1 + ν)} = \frac{3 (1 - 2 \times 0 .495)}{0 .36 (1 + 0 .495)} = 0.055741$

$\frac{1}{D 1} = 17.94$

C10 . . . . . . . . . . . . . . . . . . .= 0.1800000000000    
     C01 . . . . . . . . . . . . . . . . . . .=  0.000000000000    
     C20 . . . . . . . . . . . . . . . . . . .=-2.0000000000000E-03
     C11 . . . . . . . . . . . . . . . . . . .=  0.000000000000    
     C02 . . . . . . . . . . . . . . . . . . .=  0.000000000000    
     C30 . . . . . . . . . . . . . . . . . . .= 5.0000000000000E-05
     C21 . . . . . . . . . . . . . . . . . . .=  0.000000000000    
     C12 . . . . . . . . . . . . . . . . . . .=  0.000000000000    
     C03 . . . . . . . . . . . . . . . . . . .=  0.000000000000    
     1/D1  . . . . . . . . . . . . . . . . . .=  17.94001716615    
     1/D2  . . . . . . . . . . . . . . . . . .=  0.000000000000    
     1/D3  . . . . . . . . . . . . . . . . . .=  0.000000000000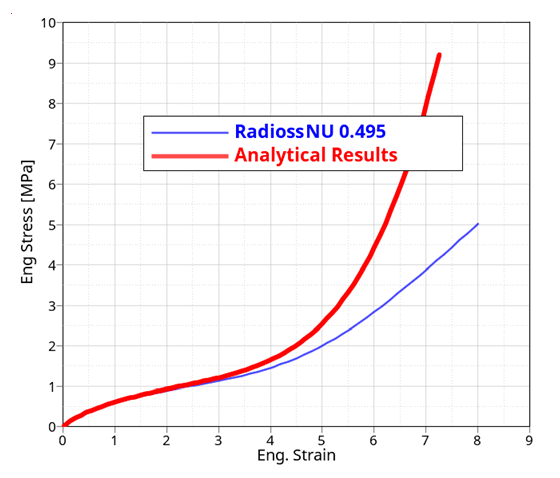

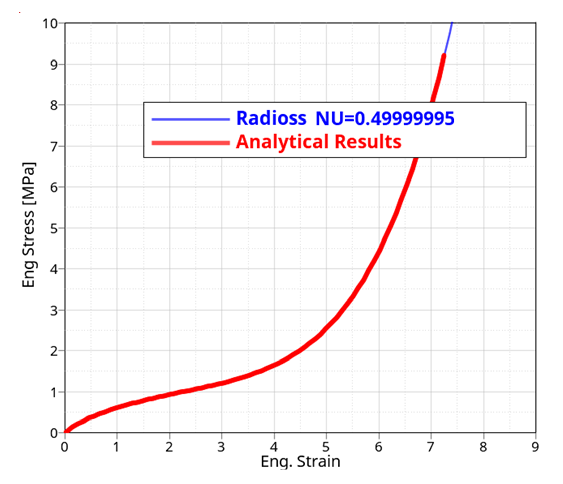
Compare the above results, then show the difference with analytical results especially in high deformed area.

In order to match the incompressible hyperelastic analytical results, the Poisson’s ratio needs to be defined as close to 0.5 as possible, but can not be simply defined as

$ν =0 .5$ , which will lead to infinite small time step in numerical computation. In this example

$ν = 0.49999995$ is used. It shows Radioss results are well matched with analytical results.

Since material incompressible is assumed in analytical calculation., Poisson’s ratio closer to 0.5 is better, but the computation time will increase. Just one element tension model from $ν =0 .495$ to $ν = 0.49999995$ run time is more than 20 times increased. In this example, use $ν =0 .4997$ ; therefore, set D1=0.003334.