Home
Altair HyperWorks Tools
Administrative tools to customize your Altair HyperWorks installation.
Model Identification Tool
The Model Identification Tool (MIT) is a profile in HyperGraph for fitting test data from frequency- and amplitude-dependent bushings to analytical models. The MIT operates in conjunction with HyperGraph, MotionView and MotionSolve to provide you with a comprehensive solution for modeling and analysis.
Altair Bushing Model
The Altair Bushing Model is a library of sophisticated, frequency- and amplitude-dependent bushing models that you can use for accurate vehicle dynamics, durability and NVH simulations. The Altair Bushing Model supports both rubber bushings and hydromounts.
Sprague-Geers Metric for Data Similarity
This section defines and provides examples of the Sprague-Geers Metric for Data Similarity.

What's New
View new features for Altair HyperWorks 2024.
Altair HyperWorks Introduction
Quick introduction to Altair HyperWorks products.
Tutorials
Discover the functionality of Altair HyperWorks products with interactive tutorials.
Altair HyperWorks Tools
Administrative tools to customize your Altair HyperWorks installation.
- Altair License Utility
  Use the Altair License Utility to determine a managed Altair Licensing ID, check license usage, borrow licenses, and set up managed Altair Units.
- Altair Compute Console
  Altair Compute Console (ACC) is a utility that allows you to start different Altair HyperWorks Solvers.
- Remote Job Submission
  Remote Job Submission in Altair Compute Console (ACC) is implemented as an alternative to a local run.
- Remote Server User Guide
- AbaqusODB Upgrade
  AbaqusODB UpGrade is a HyperView tool, which upgrades ODB files created in Abaqus 2018 (or earlier) to Abaqus 2023.
- HgTrans
  HgTrans translates solver results files from their native file format to Altair Binary Format (ABF). This can be done using the HgTrans GUI or via the HgTrans batch mode.
- HvTrans
  HvTrans is a result translator for HyperView that translates solver result files to .h3d files.
- HWTK GUI Toolkit
  The HWTK GUI Toolkit is a resource tool for coding Tcl/Tk dialogs. It contains documentation of the HWTK GUI Toolkit commands, demo pages that illustrate our Altair GUI standards, and sample code for creating those examples.
- Cleanup Utility
  The Cleanup Utility is a script for Windows that removes any custom settings that you may have due to the Altair applications installed.
- Model Identification Tool
  The Model Identification Tool (MIT) is a profile in HyperGraph for fitting test data from frequency- and amplitude-dependent bushings to analytical models. The MIT operates in conjunction with HyperGraph, MotionView and MotionSolve to provide you with a comprehensive solution for modeling and analysis.
  - MIT and the Fitting Process
  - Start MIT
    This section explains how to start the MIT interactively and in batch mode.
  - Use MIT
    This section explains how to use the features in HWTK GUI Toolkit.
  - Appendix I: SPD File Format Specification
  - Altair Bushing Model
    The Altair Bushing Model is a library of sophisticated, frequency- and amplitude-dependent bushing models that you can use for accurate vehicle dynamics, durability and NVH simulations. The Altair Bushing Model supports both rubber bushings and hydromounts.
    - Types of Bushing Models
      MIT supports three types of bushing models for static stiffness and three types for damping effects.
    - Steady State Response of Nonlinear Systems
      Bushing measurements are typically provided in the frequency domain, and not in the time domain. Thus, for a given preload and frequency, the bushing is typically subjected to a sinusoidal input at a given frequency. The bushing response at steady state, for the given preload and frequency, is measured in terms of a dynamic stiffness (K_d ) and a loss angle ( $ϕ$ ).
    - Fitting a Nonlinear, Dynamic System
      This section describes the fitting process and the main challenges associated with it for a nonlinear, dynamic system.
    - Units Conversion
      The quantities in the .spd, .gbs and .opt files are units dependent. In order to provide the greatest generality, MIT supports units conversion.
    - Sprague-Geers Metric for Data Similarity
      This section defines and provides examples of the Sprague-Geers Metric for Data Similarity.
    - Deviation Metrics Calculations
      The Sprague-Geers method is a robust way to gauge the similarity between two sets of curves.
  - Use the Altair Bushing Model with MotionView
    This section provides information about using the Altair Bushing Model, also known as AutoBushFD, with MotionView. The Altair Bushing Model is a sophisticated model that you can use to simulate the behavior of bushings in vehicle dynamics, durability and NVH simulations.
  - Use the Altair Bushing Model with MotionSolve
    This section provides information about using the Altair Bushing Model, also known as AutoBushFD, with MotionSolve.
  - Supported Solvers
- Register HVPcontrol
  Register HVPcontrol registers the HVP ActiveX control for HyperView Player.
- HyperWorks Automation Toolkit
  The HyperWorks Automation Toolkit (HWAT) is a collection of functions and widgets that allows an application to quickly assemble HyperWorks automations with minimal effort and maximum portability.
- H3D Validation Tools
  The H3D Validation Tools available are H3D Info and H3D Validate.
- Uninstall
  Use the Altair HyperWorks Products Uninstaller to remove all files from the installation directory.

View All Altair HyperWorks Help

Sprague-Geers Metric for Data Similarity

This section defines and provides examples of the Sprague-Geers Metric for Data Similarity.

Definition

Consider two signals a(x_k) and b(x_k), k=1…N. You are interested in computing a metric that shows the similarity of these signals. Use the following steps to compute the Sprague-Geers metric:

Calculate the metric M for magnitude difference and P for phase difference as follows:
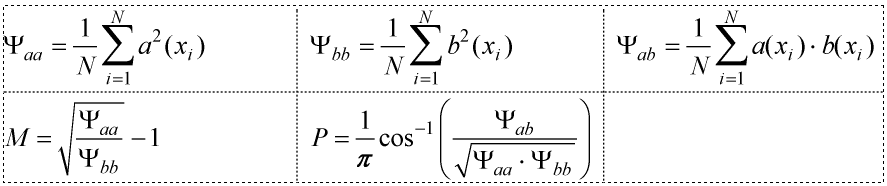
Calculate the combined metric C as follows:
$C = 1 - \sqrt{M^{2} + P^{2}}$
C=1 is a perfect match. Metric C is what we want to show.
Note: $\sqrt{M^{2} + P^{2}}$ is known as the Sprague-Geers Combined Metric.

Example 1: Signals with the same overall magnitude, but drastically different slopes

Figure 1.

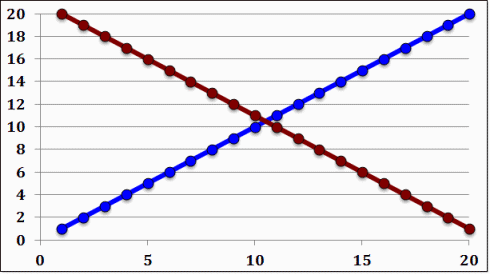
Ψ_aa=143.50, Ψ_bb=143.50, Ψ_ab=77.00, M+0.00, P=0.319714, C=0.680286

Example 2: Two very similar signals displaced in the y direction by 5%

Figure 2.

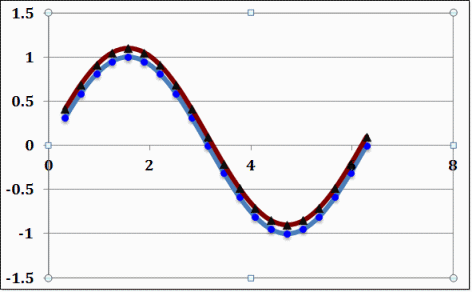
Ψ_aa=0.50, Ψ_bb=0.51, Ψ_ab=0.50, M=0.009852, P=0.044719, C=0.954208

Example 3: A synthesized MIT example for Dynamic Stiffness

Figure 3.

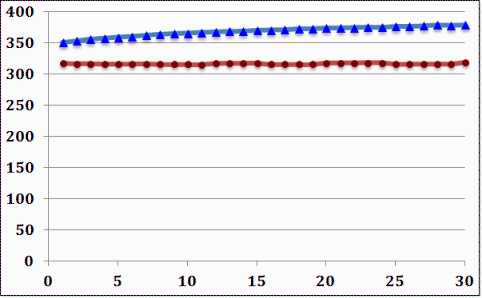
Ψ_aa=3.39E+5, Ψ_bb=3.77E+5, Ψ_ab=3.57E+5, M=0.051164, P=0.026831, C=0.942227

Example 4: A synthesized MIT example for Loss Angle

Figure 4.

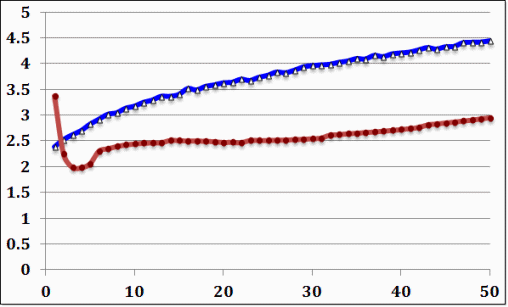
Ψ_aa=1.39628E+1, Ψ_bb=6.67958, Ψ_ab=9.59216, M=0.445811, P=0.037025, C=0.552654