HS-1035: Excelスプレッドシートを使用した最適化スタディ

HyperStudyのスプレッドシートとの連成を使用し、入力変数と出力応答の確認、およびOptimization（最適化）スタディの実行方法を学習します。

開始に先がけ、本チュートリアルで使用されるモデルファイルを<hst.zip>/HS-1035/から自身の作業ディレクトリにコピーします。
問題の定式化
  • 断面の幅と高さをmmで求める
  • 先端のひずみが0.53 mm未満となるように梁の体積を最小化

Excelスプレッドシートの確認

Excelスプレッドシートモデルを作成する際は、スプレッドシートが正しく書式設定されていることが重要です。変数の値とラベルは、2つの連続する行または連続する列に設定できます。変数ラベルは、英字、もしくは英字と数字の組み合わせしか含むことができません。変数にラベルを生成していない場合、HyperStudyがデフォルト値を割り当てます。

  1. Excelで、hst_spreadsheet_integration_example.xlsファイルを開きます。
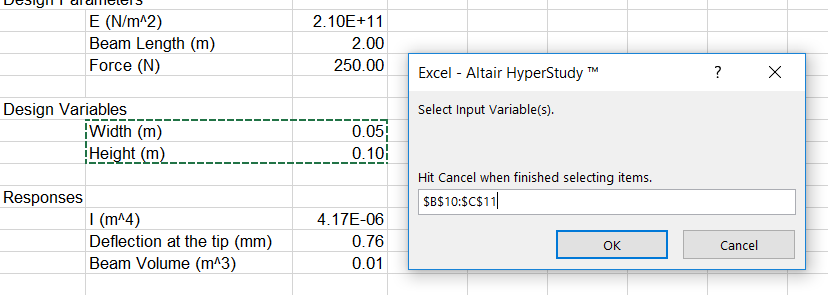
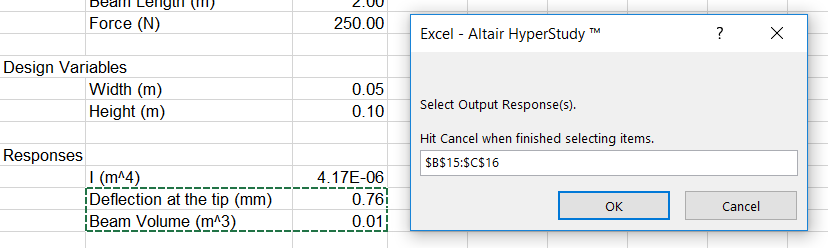
  2. 情報を確認し、入力変数と出力応答を含む列を探します。

スタディのセットアップの実行

  1. HyperStudyを開始します。
  2. 以下の方法で新規スタディを開始します：
    • メニューバーから、File（ファイル） > New（新規）をクリックします。
    • リボン上でをクリックします。
  3. Add Study（スタディの追加）ダイアログでスタディの名前を入力し、スタディの場所を選んでOKをクリックします。
  4. Define Models（モデルの定義）ステップに進みます。
  5. hst_spreadsheet_integration_exampleファイルをDirectory（ディレクトリ）からワークエリアにドラッグ＆ドロップし、スプレッドシートモデルを追加します。
    図 1.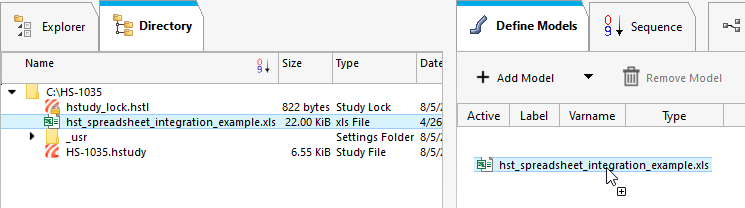


    Resource（リソース）欄とSolver input file（ソルバー入力ファイル）欄がアクティブになります。Solver input file（ソルバー入力ファイル）欄にはhst_input.hstpが表示されており、これが、評価中にHyperStudyが書き出すソルバー入力ファイルの名称となります。
  6. Import Variables（変数のインポート）をクリックします。
    hst_spreadsheet_integration_example.xlsスプレッドシートが開きます。
  7. 入力変数を追加します。
    1. ExcelダイアログでYes（はい）をクリックし、入力変数の選択を開始します。
      図 2.


    2. スプレッドシート内で、入力変数のラベルと値を含んだセルを選択します。
      図 3.


    3. Excelダイアログで、OKをクリックします。
    4. Cancel（キャンセル）をクリックして、入力変数の選択を停止します。
  8. 出力応答を追加します。
    1. ExcelダイアログでYes（はい）をクリックし、出力応答の選択を開始します。
    2. スプレッドシート内で、出力応答のラベルと値を含んだセルを選択します。
      図 4.


    3. Excelダイアログで、OKをクリックします。
    4. Cancel（キャンセル）をクリックして、出力応答の選択を停止します。
    2つの入力変数と2つ出力応答がhst_spreadsheet_integration_example.xlsスプレッドシートからインポートされます。
  9. Define Input Variables（入力変数の定義）ステップに進みます。
  10. 入力変数の下限値と上限値を確認します。

ベースランの実行

  1. Test Models（モデルをテスト）ステップに進みます。
  2. Run Definition（計算実行）をクリックします。
    スタディのDirectory（ディレクトリ）内に、approaches/setup_1-def/ディレクトリが作成されます。approaches/setup_1-def/run__00001/m_1には、ベースランの結果である入力ファイルが含まれます。

出力応答の確認

  1. Define Output Responses（出力応答の定義）パネルに進みます。
  2. スタディにインポートされた出力応答を確認します。
    出力応答が、HyperStudyが各ランについて作成したhst_output.hstpファイルから抽出されました。
    図 5.


最適化の実行

  1. Optimization（最適化）を追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
    2. Add（追加）ダイアログでOptimization（最適化）を選択します。
    3. Definition from（定義元）に、Setup（セットアップ）を選択しOKをクリックします。
  2. Optimization（最適化） > Definition（定義） > Define Input Variables（入力変数の定義）ステップに進みます。
  3. 両方の入力変数の下限および上限値に+17%のセットを適用します。
    1. 両方の入力変数の列の下限値列で、をクリックします。
    2. Percent欄に+17と入力します。
    3. +/-ボタンをクリックします。
    4. 適用（適用）.をクリックします。
    図 6.


  4. Optimization（最適化） > Definition（定義） > Define Output Responses（出力応答の定義）ステップに進みます。
  5. Objectives/Constraints - Goals（目的 / 制約条件 - 目標）タブをクリックします。
  6. Beam Volume (m^3)出力応答に目的関数を割り当てます。
    1. Add Goal（目標を追加）をクリックします。
    2. Apply On（応答）列で、Beam Volume (m^3)を選択します。
    3. Type （タイプ）列に、Minimizeを選択します。
    図 7.


  7. 制約条件をDeflection at the tip (mm)応答出力に割り当てます。
    1. Add Goal（目標を追加）をクリックします。
    2. Apply On（応答）列で、Deflection at the tip (mm)を選択します。
    3. Type （タイプ）列に、Constraintを選択します。
    4. column 1に<=（以下）を選択します。
    5. column 2に0.53と入力します。
    図 8.


  8. Optimization（最適化） > Specifications（スタディ仕様）ステップに進みます。
  9. ワークエリア内でModes（モード）をAdaptive Response Surface Method （逐次更新型応答曲面法）(ARSM)にセットします。
    注: 問題の定式化に有効な手法のみが使用可能です。
  10. 適用をクリックします。
  11. Evaluate（評価）ステップに進みます。
  12. Evaluate Tasks（計算実行）をクリックします。
  13. 最適化中に評価されたすべてのランの入力変数値、出力応答、目的関数および制約条件の値を確認します。
    • すべての入力変数および出力応答の詳細サマリーを一覧で確認するには、Evaluation Data（評価データ）タブをクリックします。
    • 各ランについて、入力変数と出力応答の値の２次元グラフをプロットするには、Evaluation Plot（評価プロット）をクリックします。
    図 9. 評価プロット


  14. 最適化中に評価された各反復計算の入力変数値、出力応答、目的関数および制約条件の値を確認します。
    Channel（チャンネル）セレクターを使って、表示すべき入力変数、出力応答、目標などを選択します。
    • Iteration History（反復計算履歴）タブをクリックし、反復履歴の詳細サマリーを確認します。
      このスタディはARSMで実行されたため、評価データと反復計算履歴の両方で同じ設計が見られます。この反復計算の一覧から、反復計算1、2、5が、制約違反があっていることを示す赤いフォントで表示されていることがわかります。制約違反のある制約条件Constraint 1が赤い太字のフォントで表示されています。反復計算3、4、および6-8は、現実的ではあるものの、最適設計ではありません。反復計算9は、緑色でハイライト表示されており、これは、設計が最適化設計であることを意味します。
      図 10.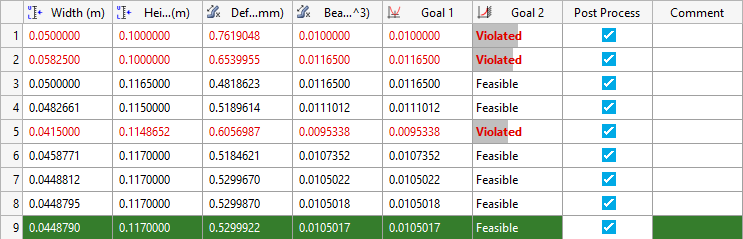


    • Iteration Plot（反復計算プロット）タブをクリックし、反復計算履歴をプロットします。
      図 11. Goal 1（目的関数）とGoal 2（制約条件）の反復計算プロット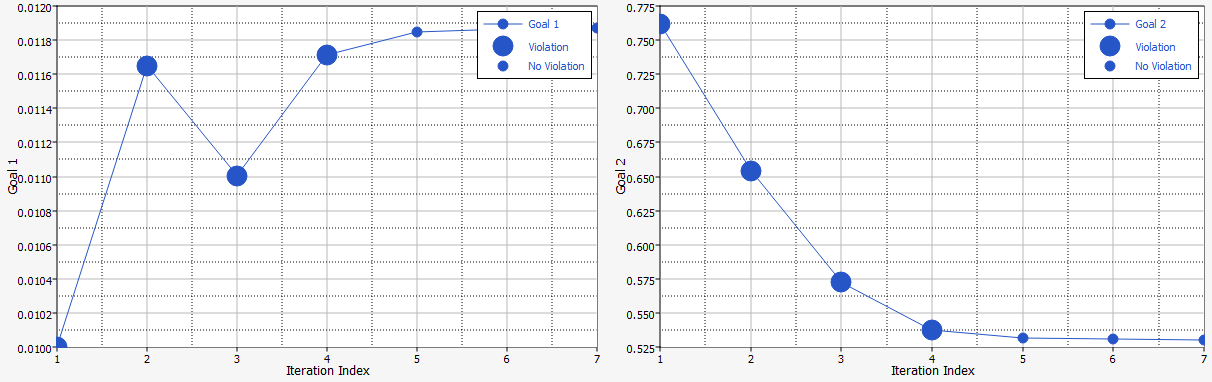


      1つ目のプロット（Goal 1）では、実現不可能な設計が大きいマーカーで確認できます。2つ目のプロット（Goal 2）では、これらの設計は制約境界である0.53より高い変位置を有しており、最後の３つの設計のみが制約境界を満たしています。