HS-1050： 外部Rosenbrock関数の最小化

ComposeまたはPythonを用いて2D Rosenbrock関数を最適化する方法について学習します。

開始に先がけ、本チュートリアルで使用されるモデルファイルを<hst.zip>/HS-1050/から自身の作業ディレクトリにコピーします。

本チュートリアルは、xおよびyとラベル付けされた2つの設計変数を定義します。

最適化の目的は、 f(x,y)= 100*(y-x^2)^2 + (1-x)^2 を最小にすることです。xとyの範囲は[-2 ; -2]、開始ポイントは[-1 ; -1]に設定されます。

スタディのセットアップの実行

  1. HyperStudyを開始します。
  2. 以下の方法で新規スタディを開始します：
    • メニューバーから、File（ファイル） > New（新規）をクリックします。
    • リボン上でをクリックします。
  3. Add Study（スタディの追加）ダイアログでスタディの名前を入力し、スタディの場所を選んでOKをクリックします。
  4. Define Models（モデルの定義）ステップに進みます。
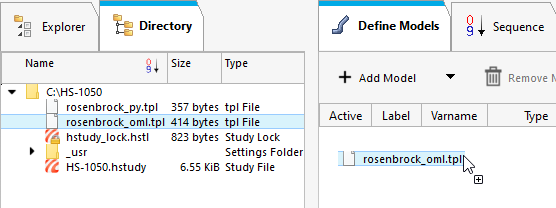
  5. パラメータ化ファイルモデルを1つ追加します。
    1. Directory（ディレクトリ）から、適切な.tplファイルをワークエリアにドラッグ＆ドロップします。
      • Pythonをご使用の場合は、rosenbrock_py.tplファイルを用います。
      • Composeをご使用の場合は、rosenbrock_oml.tplファイルを用います。
      図 1.


    2. Solver Input File（ソルバー入力ファイル）列に、HyperStudyが評価中に書き出すソルバー入力ファイルの名称を入力します。
      • Pythonをご使用の場合は、rosenbrock.pyと入力します。
      • Composeをご使用の場合は、rosenbrock.omlと入力します。
    3. 上記の選択に応じ、Solver execution script（ソルバー実行スクリプト）列に、Python (py)またはCompose (oml)を選択します。
      注: Composeを同じソフトウェアグループとしてご使用の場合は自動的に正しい.batファイルを指します。Composeを個別にインストールとされている場合は、Register Solver Script（ソルバースクリプトの登録）ステップでCompose_batch.batを指定する必要があります。
    4. ソルバー実行スクリプトとしてComposeをご使用の場合、Solver input arguments（ソルバー引数）列に-f infront ${file}と入力します。
      注: Linux上でのソルバースクリプトの場合、Composeバッチモードをバックグラウンドではなくフォアグラウンドで稼動させるには、Solver input arguments（ソルバー引数）列に"-f ${file} -nobg"と入力します。
  6. Import Variables（変数のインポート）をクリックします。
    ２つの入力変数が.tplファイルからインポートされます。
  7. Define Input Variables（入力変数の定義）ステップに進みます。
  8. 入力変数の下限値、初期値、上限値を、図 2内に示す数値に変更します。
    図 2.


ベースランの実行

  1. Test Models（モデルをテスト）ステップに進みます。
  2. Run Definition（計算実行）をクリックします。
    スタディのDirectory（ディレクトリ）内に、approaches/setup_1-def/ディレクトリが作成されます。approaches/setup_1-def/run__00001/m_1には、ベースランの結果である入力ファイルが含まれます。

出力応答の作成と評価

このステップでは出力応答を1つ生成します。

  1. Define Output Responses（出力応答の定義）パネルに進みます。
  2. Directory（ディレクトリ）から、approaches/setup_1-def/run__00001/m_1にあるrosenbrock.resファイルをワークエリアにドラッグ＆ドロップします。
  3. File Assistant（ファイルアシスタント）ダイアログで、Reading technology（読み取り技術）をAltair® HyperWorks®にセットし、Next（次）をクリックします。
  4. Single Item in a Time Series（タイムシリーズの単一アイテム）を選択し、Next（次）をクリックします。
  5. 以下のオプションを定義し、Next（次）をクリックします。
    1. TypeをUnknownにセットします。
    2. RequestをBlock 1にセットします。
    3. ComponentをColumn 1にセットします。
    図 3.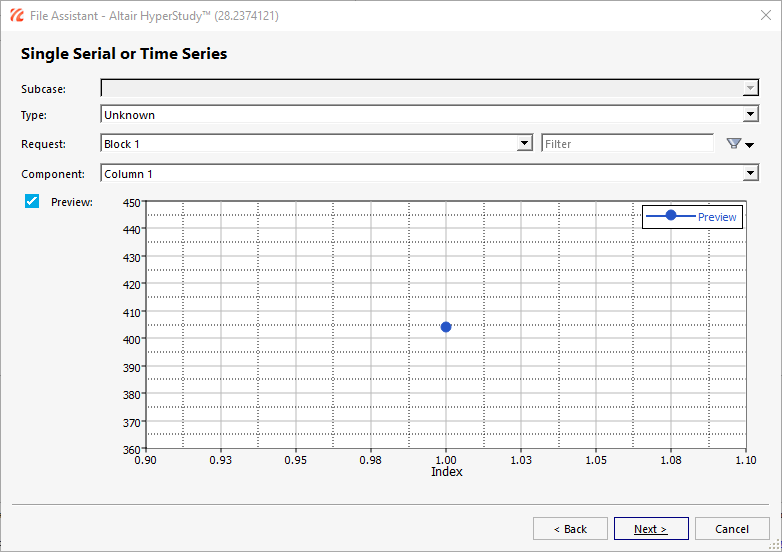


  6. オプション: データソースと出力応答のラベルを入力します。
  7. Expression（式）をFirst Element（最初の要素）にセットします。
    式がm_1_ds_1[0]に変わります。
  8. Finish（終了）をクリックします。
    図 4.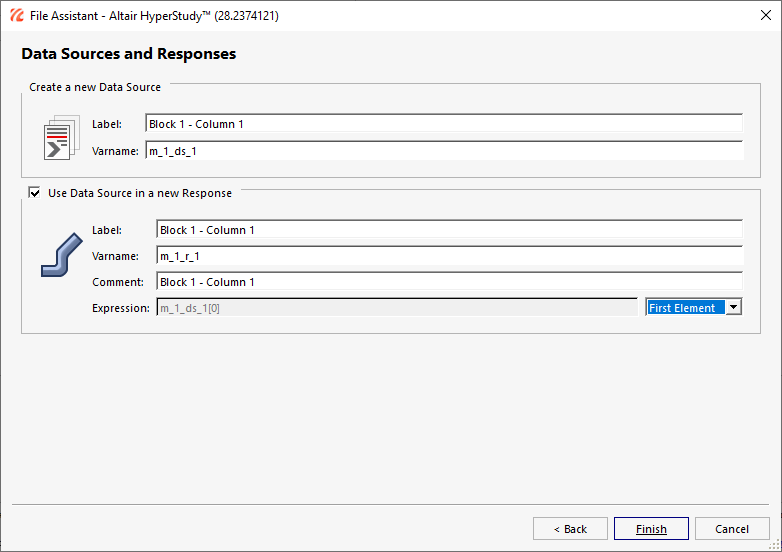


    出力応答1がワークエリアに追加されます。
  9. Evaluate（評価）をクリックします。
    式m_1_ds_1[0]の値は404.0となるはずです。

最適化の実行

  1. Optimization（最適化）を追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
    2. Add（追加）ダイアログでOptimization（最適化）を選択します。
    3. Definition from（定義元）に、Setup（セットアップ）を選択しOKをクリックします。
  2. Optimization（最適化） > Definition（定義） > Define Output Responses（出力応答の定義）ステップに進みます。
  3. Objectives/Constraints - Goals（目的 / 制約条件 - 目標）タブをクリックします。
  4. Response 1に目的関数を追加します。
    1. Add Goal（目標を追加）をクリックします。
    2. Type （タイプ）列に、Minimizeを選択します。
    図 5.


  5. Optimization（最適化） > Specifications（スタディ仕様）ステップに進みます。
  6. ワークエリア内でModes（モード）をAdaptive Response Surface Method （逐次更新型応答曲面法）(ARSM)にセットします。
    注: 問題の定式化に有効な手法のみが使用可能です。
  7. Apply（適用）をクリックします。
  8. Evaluate（評価）ステップに進みます。
  9. Evaluate Tasks（計算実行）をクリックします。
  10. オプション: Iteration Plot（反復計算プロット）タブをクリックし、最適化の進捗を確認します。
    反復計算履歴は、目的関数値の大きな減少を示しています。Rosenbrock関数は、真の最適の領域での平坦さのため、いかなる最適化エンジンにおいても探し出すのが困難であるグローバルの最小値を有しており、ARSMは (x,y)=(1,1)における理論解を見つけていません。
    図 6.