HS-3000： フィット手法の比較：　アームモデルの近似

チュートリアルで紹介されたアームモデルの出力応答の近似を作成し、異なるフィット手法間における差異について確認する方法について学習します。

開始に先がけ、HS-2000： DOE化手法の比較: アームモデルのスタディを完了するか、もしくは<hst.zip>/HS-3000/にあるHS-2000.hstxアーカイブファイルをインポートします。

HS-2000： DOE化手法の比較: アームモデルのスタディでは、9つの入力変数ではなく6つの入力変数で同程度に効果的にスタディを継続できることが分かりました。他の変数は出力応答にそれほどの影響を及ぼさないためです。これは、計算の負荷を軽減します。

本チュートリアルでは6つの形状変数を使用します。
  • Length1： Lower Bound = -0.5, Initial Bound = 0.0, Upper Bound = 2.0
  • Length2：Lower Bound = 0.0, Initial Bound = 0.0, Upper Bound = 2.0
  • Length3：Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
  • Length4：Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
  • Length5：Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
  • Height: Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0

MELS DOEスタディの実行

このステップでは、Modified Extensible Lattice Sequence（修正済み拡張格子配列） （Mels） DOEを作成します。このマトリックスを使って、両方の出力応答についてフィットを作成します。

MELSは、サンプリングポイントの集中や空白を最小限にすることによってポイント群を均等に分散させるために設計された空間充填DOE手法です。N個の変数を有する２次多項式を作成するのに必要な最小限のポイント数は、1.1*(N + 1)*(N + 2)/2 です。

代用モデルとして使用される近似を作成するために、入力マトリックスとして機能する特定のDOEを実行する必要があります。MELSなど、応答曲面作成で使用されるにふさわしいDOEを実行しなくてはなりません。

  1. DOEを追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
      Add（追加）ダイアログが開きます。
    2. Select Type（タイプの選択）からDOEを選択します。
    3. Definition from（定義元）に、アプローチを選択します。
    4. Setup（セットアップ）を選択し、OKをクリックします。
  2. 入力変数を修正します。
    1. Setup > Definition（定義） > Define Input Variables（入力変数の定義）ステップに進みます。
    2. ワークエリアのActive（アクティブ）列で、radius_1、radius_2、およびradius_3のチェックマークを外します。
    図 1.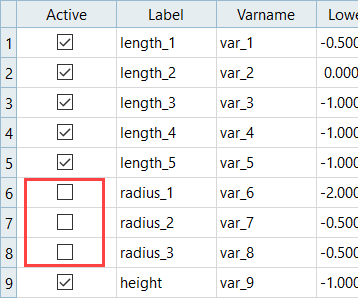


  3. スタディ仕様を定義します。
    1. DOE 5 > Specifications（スタディ仕様）ステップに進みます。
    2. ワークエリアで、Modes（モード）をModified Extensible Lattice Sequence （修正済み拡張格子配列）(MELS)にセットします。実行の数を31に設定します。
    3. Settings（セッティング）タブで、Number of Runs（実行の数）が31となっていることを確認します。
    4. Apply（適用）をクリックします。
  4. タスクを評価します。
    1. DOE 5 > Evaluate（評価）ステップに進みます。
    2. Evaluate Tasks（計算実行）をクリックします。
  5. DOE 5 > Post Processing（ポスト処理）ステップに進みます。
  6. Scatter（散布図）タブをクリックし、MELS DOEからの結果の2D散布図を確認します。
    図 2. 31のラン（length_1 vs. length_2）のMELS DOEの典型的なサンプリング. この図は、6つの側面に分散された31個のポイントの2次元平面への投影です。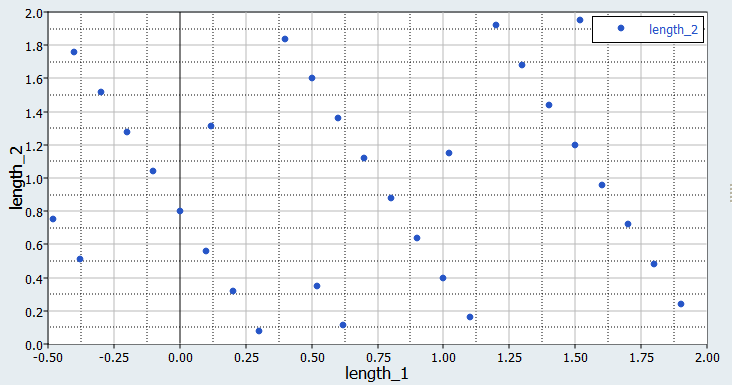


オプション：より少ない実行数でのDOEの実行

このステップではオプションとして、フィットアプローチでの検証マトリックスとして使用するために、より少ない実行数で2つ目のDOEを作成します。

検証マトリックスは、フィットの予測精度についての情報を提供します。
注: 検証マトリックスとしてMELSを使用してはいけません。これは、その拡張性により、MELS入力マトリックスからの同じ１つ目の実行を取るためです。

本チュートリアルでは、検証マトリックスの作成に、Hammersleyを使用します。

  1. DOEを追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
      Add（追加）ダイアログが開きます。
    2. Definition from（定義元）に、DOE 5を選択します。
    3. DOEを選択します。
    4. OKをクリックします。
  2. スタディ仕様を定義します。
    1. DOE 6 > Specifications（スタディ仕様）ステップに進みます。
    2. ワークエリア内でモードをHammersleyにセットします。
    3. Settings（セッティング）タブで、Number of Runs（実行の数）を12に変更します。
      図 3.


    4. Apply（適用）をクリックします。
  3. タスクを評価します。
    1. DOE 6 > Evaluate（評価）ステップに進みます。
    2. Evaluate Tasks（計算実行）をクリックします。

フィットスタディの実行

このステップでは、MELS DOEからの31のランを入力マトリックスとして、また、Hammersley DOEからの12のランを検証マトリックスとして使用し、最小自乗回帰法（LSR）、移動最小自乗法（MLSM）、HyperKriging近似（HK）および放射基底関数（RBF）を用いて4つのフィットを作成します。

  1. Fit（フィット）を追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
    2. Add（追加）ダイアログで、Fit Existing DataFit（既存データフィット）とSetup（セットアップ）を選択し、OKをクリックします。
  2. マトリックスをインポートします。
    1. Fit > Specifications（スタディ仕様）ステップに進みます。
    2. Add Matrix（マトリックスの追加）を2回クリックします。
    3. ワークエリアで、図 4に示されるオプションを選択し、Fit Matrix 1とFit Matrix 2を定義します。
    4. 適用（適用）をクリックします。
    図 4.


  3. スタディ仕様を定義します。
    1. ワークエリアのFit Type（近似手法）列で、適切なフィット手法を選択します。
      重要:

      Least Sqaure Regressions（最小自乗回帰法）（LSR）フィットについて、Settings（セッティング）タブで、Interaction（交互作用）を交互作用にセットします。

      交互作用回帰式モデルは、関数f(x,y)=A+Bx+Cy+Dxy内の線形および交差項が考慮されることを可能にします。ここで、最初の３つの項は線形、最後の項は変数間の交差項です。

    2. 適用（適用）をクリックします。
  4. タスクを評価します。
    1. Fit > Evaluate（評価）ステップに進みます。
    2. Evaluate Tasks（計算実行）をクリックします。
  5. Fit > Post Processing（ポスト処理）ステップに進みます。
  6. Scatter（散布図）タブをクリックし、元のMax_Stress出力応答とフィットMax_Stressを比較します。

    散布図は、フィットの精度を表します。ポイント群が対角線に近いほど、フィットは良好です。Max_Stress vs Max_Stress_LSRのプロットでは、分散したポイント群も一部見られます。これは、フィットが部分的に精確ではないことを表しています。それに対し、Max_Stress vs Max_Stress_MLSMのプロットは、より対角線に沿っています。これは、Max_Stressについてフィットの精度が高いことを示しています。

    散布図を使ったHyperKrigingとRadial Basis Functionの比較は行いません。これは、結果が誤っている可能性があるためです。HyperKrigingとRadial Basis Functionはデフォルトでポイントそのものを通過するため、元の出力応答とフィットの出力応答を比較する散布図は直線となります。しかしながら、これは必ずしも、フィットが良好な予測能力を有することを意味しません。
    図 5. Max_stressとMax_stress、LSRの比較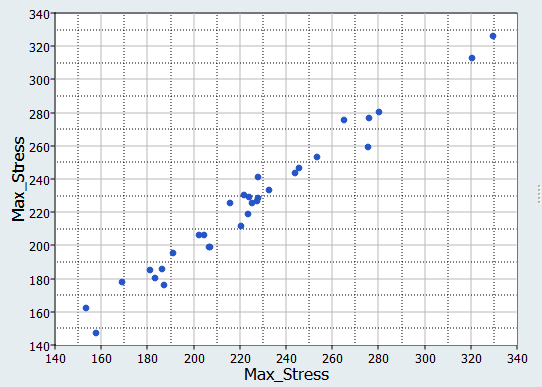


    図 6. Max_stressとMax_stress、MLSMの比較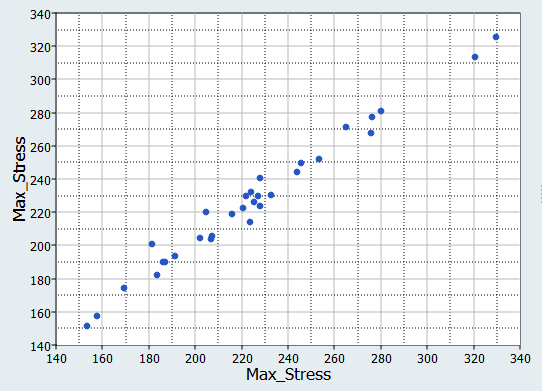


  7. Diagnostics（診断）タブをクリックし、フィットスタディの診断を確認します。
    決定係数値は、応答データの平均値周りのばらつきがどれだけ捕捉されているかの尺度となります。モデルが既知の値を完全に予測している場合、決定係数は可能である最大の値である1.0を示します。
    図 7. Max_Stress、LSRの診断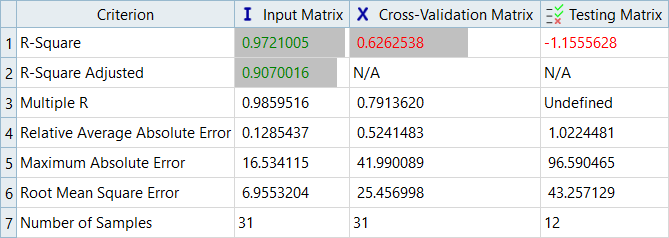


    図 8. Max_Stress、MLSMの診断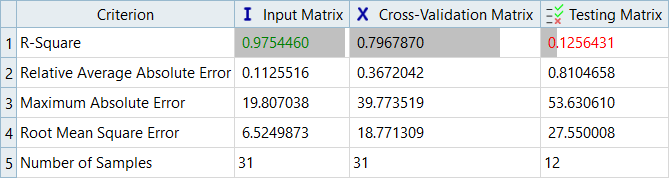


    HyperKrigingとRadial Basis Functionでの入力マトリックスの決定係数値は意味を持ちません。これは、実行がデータポイントそのものを通過するために、値が1.0となるためです。値が1.0であっても、これは、フィットが精確であることを意味してはいません。HyperKrigingとRadial Basis Functionでは、意味のある診断値は、交差検証マトリックスと検証マトリックスのみです。
    図 9. Max_Stress、HKの診断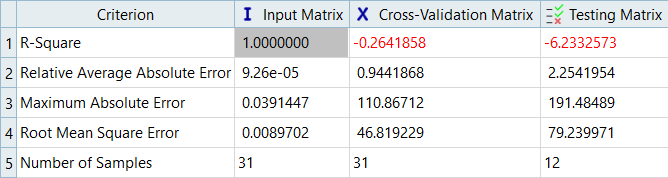


    図 10. Max_Stress、RBFの診断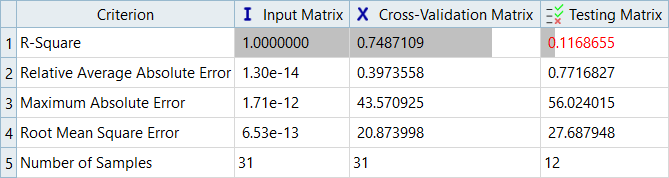


  8. Residuals（残差）タブをクリックし、元の出力応答とフィットの出力応答との間の誤差および誤差（％）を、それぞれの入力および検証マトリックスの各実行について確認します。
    図 11. Max_Stress、LSRの入力マトリックスの残差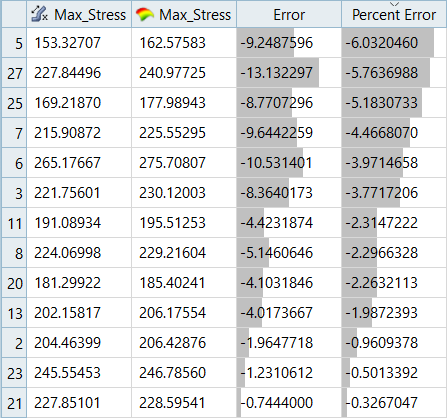


    図 12. Max_Stress、LSRのテストマトリックスの残差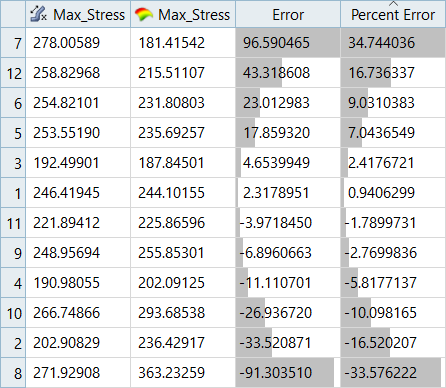


    入力マトリックスの残差の誤差は、Least Square RegressionではMoving Least Square Methodと比べてやや小さくなっていますが、テストマトリックスの残差の誤差はMoving Least Square Methodのほうがかなり小さくなっています。
    図 13. Max_Stress、MLSMの入力マトリックスの残差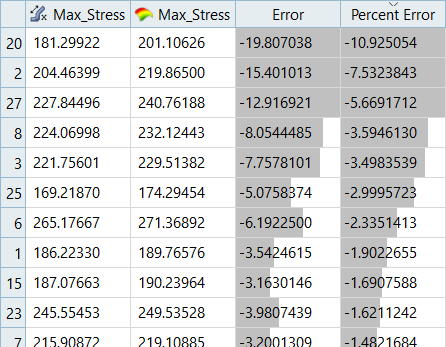


    図 14. Max_Stress、MLSMのテストマトリックスの残差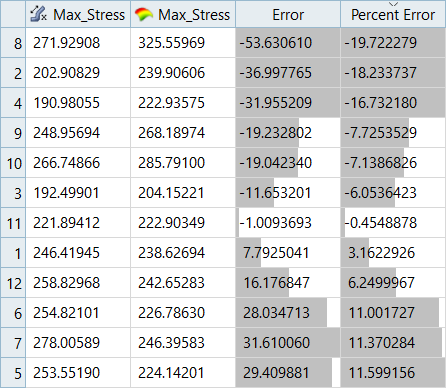


    入力マトリックスの残差は、HyperKrigingとRadial Basis Functionでは、下のテストマトリックスの残差で示すとおり、意味を持ちません。
    図 15. Max_Stress、HKのテストマトリックスの残差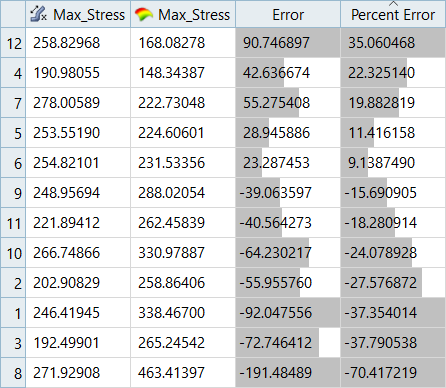


    図 16. Max_Stress、RBFのテストマトリックスの残差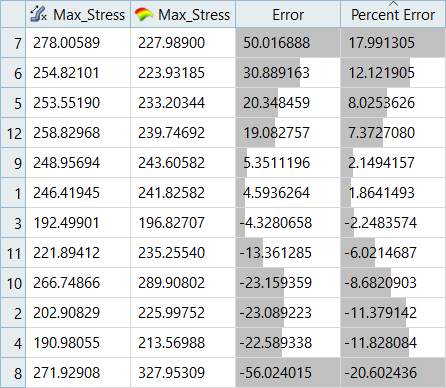


フィットの比較

入力およびテストマトリックスの誤差の最大パーセントの確認。

表 1. 入力マトリックスの残差
LSR（交互作用回帰モデル） MLSM HK RBF
Max_Disp -1.18% -2.79% - -
Max_Stress -6.72% -10.92% - -
表 2. テストマトリックスの残差
LSR（交互作用回帰モデル） MLSM HK RBF
Max_Disp 7.26% -3.00% 9.57% -2.45%
Max_Stress 34.74% -19.72% 35.06% 17.99%

Max_Dispの誤差（％）はMax_Stressのそれより小さいことが分かります。これらの結果は、フィットアプローチがMax_Dispについては良好に機能しているものの、Max_Stressについてはあまり効率がよくないことを示しています。

これは、Max_DispについてはMLSMから得られたフィットモデルを用いるのがベストであることを示唆しています。Max_Stressのような出力応答は、局所化された効果の全体的な包絡です。出力応答のそのような包絡タイプの特性は、フィットでの精確な捕捉を困難にします。一方、Max_Disp出力応答は、局所化された効果によって影響を受けないため、そのようなデータにはより容易にフィットを用いることができます。このようなケースを処理する際、サンプル数を増やすことが推奨されます。これは、精度を上げる、または入力変数のより単純な関数、たとえば、特定の領域をそれぞれ捕捉するいくつかの出力応答など、より局所化された一連の出力応答の作成を保証するものではありません。下の図は、入力マトリックスでの実行から得られた応力の高い領域をハイライト表示しています。
図 17.