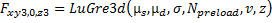Force: Joint Friction

フォーマット

<Force_JointFriction
     id                        = "integer"   
   [ label                     = "string" ]     
     joint_id                  = "integer"
     mu_static                 = "real"
     mu_dynamic                = "real"   
   [ max_stiction_deform       = "real" ]
   [ bristle_stiffness         = "real" ]
   [ damping_effects           = "real" ]   
   [ viscous_effects           = "real" ]
   [ stiction_trans_vel        = "real"]
   [ inactive                  = "None | Static" ]
   [ effect                    = "All|Stiction |Sliding" ]
   [ inputs                    = "4-bit integer" ]
   [ torque_preload            = "real" ]
   [ friction_arm              = "real" ]
   [ bending_reaction_arm      = "real" ]
   [ pin_radius                = "real" ]
/>

<Force_JointFriction
     id                        = "integer"   
   [ label                     = "string" ]     
     joint_id                  = "integer"
     mu_static                 = "real"
     mu_dynamic                = "real"    
   [ max_stiction_deform       = "real" ]   
   [ bristle_stiffness         = "real" ]
   [ damping_effects           = "real" ]
   [ viscous_effects           = "real" ]
   [ stiction_trans_vel        = "real"]
   [ inactive                  = "None |Static" ]
   [ effect                    = "All |Stiction|Sliding" ]
   [ inputs                    = "4-bit integer" ]    
   [ torque_preload            = "real" ]
   [ ball_radius               = "real" ]
/>

<Force_JointFriction
     id                        = "integer"   
   [ label                     = "string" ]     
     joint_id                  = "integer"
     mu_static                 = "real"
     mu_dynamic                = "real"    
   [ max_stiction_deform       = "real" ]
   [ bristle_stiffness         = "real" ]   
   [ damping_effects           = "real" ]
   [ viscous_effects           = "real" ]
   [ stiction_trans_vel        = "real" ]
   [ inactive                  = "None|Static"]
   [ effect                    = "All|Stiction|Sliding" ]
   [ inputs                    = "4-bit integer" ]     
   [ force_preload             = "real" ]
   [ reaction_arm              = "real" ]
   [ initial_overlap           = "real" ]
   [ overlap_delta             = "Constant|Increase|Decrease" ]
/>

<Force_JointFriction
     id                        = "integer"   
   [ label                     = "string" ]     
     joint_id                  = "integer"
     mu_static                 = "real"
     mu_dynamic                = "real"    
   [ max_stiction_deform       = "real" ]
   [ bristle_stiffness         = "real" ]
   [ damping_effects           = "real" ]
   [ viscous_effects           = "real" ]
   [ stiction_trans_vel        = "real"]
   [ inactive                  = "None|Static"]
   [ effect                    = "All|Stiction|Sliding" ]
   [ inputs                    = "4-bit integer" ]
   [ force_preload             = "real" ]
   [ torque_preload            = "real" ]
   [ pin_radius                = "real" ]
   [ initial_overlap           = "real" ]
   [ overlap_delta             = "Constant|Increase|Decrease" ]
/>

<Force_JointFriction
     id                        = "integer"   
   [ label                     = "string" ]     
     joint_id                  = "integer"
     mu_static                 = "real"
     mu_dynamic                = "real"    
   [ max_stiction_deform       = "real" ]
   [ bristle_stiffness         = "real"]   
   [ damping_effects           = "real"]   
   [ viscous_effects           = "real"]   
   [ stiction_trans_vel        = "real"]   
   [ inactive                  = "None|Static"]
   [ effect                    = "All|Stiction|Sliding"]
   [ inputs                    = "4-bit integer" ]
   [ torque_preload            = "real" ]
   [ friction_arm              = "real" ]
   [ bending_reaction_arm      = "real" ]
   [ pin_radius                = "real" ]
   [ yoke_choice               = "i_yoke|j_yoke"]
/>

属性

id

要素識別番号（整数 > 0）。この番号は、すべてのForce_JointFriction要素の中で一意です。

label

要素の説明を含む文字列。

joint_id

摩擦力が適用されるジョイントのジョイントIDを指定します。

mu_static

ジョイントの静摩擦係数(μ_s)を指定します。

mu_static > 0。

デフォルト：NONE

mu_dynamic

ジョイントの動摩擦係数(μ_d)を指定します。

mu_dynamic > 0。

デフォルト：NONE

max_stiction_deform

ジョイントで静摩擦に対して生じる可能性のある最大変形を指定します。

ゼロ以外の値を指定した場合、相対速度がゼロであっても有限の静摩擦力が適用されます。

デフォルト = 0.01長さ単位

stiction_trans_vel

動摩擦から静摩擦に移行する、以下の絶対速度の実数値。

デフォルト = 0.1長さ / 時間

inactive

静解析でジョイント摩擦を無効にするには、“STATIC”を指定します。

デフォルト：NONE

effect

摩擦効果を指定します。デフォルトでは、静摩擦と動摩擦の両方が考慮されます。スティクションでは静摩擦のみが使用され、滑りでは動摩擦のみが使用されます。

デフォルト：ALL

inputs

4ビットの整数値で、摩擦モデルに入力する力を指定します。デフォルトでは、プリロードとジョイント反力がすべて含まれます。有効な値は各ビットに対して0または1です。

デフォルト：1111

次の4つの選択肢があります：

• 1番目のビット：Preload
• 2番目のビット：Reaction_Force
• 3番目のビット：Bending_Moment
• 4番目のビット：Torsional_Moment

入力値の各ビットに0または1を設定することで、個々の入力を制御します。

したがって次のようになります：

• 1111 - 4つすべての入力が含まれます。
• 0000 - 4つの入力のいずれも含まれません。
• 1000 - Preloadのみが含まれます。
• 1101 - Preload、Reaction_Force、およびTorsional_Momentは含まれますが、Bending_Momentは含まれません。
• 1001 - PreloadおよびTorsional_Momentは含まれますが、Reaction_ForceおよびBending_Momentは含まれません。

ジョイントタイプごとに使用可能なオプションは、以下に示すとおりです：

• 並進 - Preload、Reaction_Force、Bending_Moment、Torsional_Moment
• 円筒、回転、ユニバーサル、フック - Preload、Reaction_Force、Bending_Moment
• 球 -Preload、Reaction_Force

force_preload

並進および円筒ジョイントのプリロード摩擦力を指定します。

デフォルト：0.0力単位

torque_preload

回転、円筒、ユニバーサル、および球ジョイントのプリロード摩擦トルクを指定します。

デフォルト：0.0力*長さ単位

friction_arm

回転およびユニバーサルジョイントの軸摩擦トルクの計算に使用するモーメントアームを指定します。

デフォルト：1.0長さ単位

reaction_arm

並進ジョイントのアキシャル軸周りの反トルクのモーメントアームを指定します。

デフォルト：1.0長さ単位

bending_reaction_arm

回転、フック、およびユニバーサルジョイントの曲げモーメントを計算するためのモーメントアームを指定します。

デフォルト：1.0長さ単位

pin_radius

回転、円筒、フック、およびユニバーサルジョイントのピンの半径を指定します。

デフォルト：1.0長さ単位

ball_radius

球ジョイントの半径を指定します。

デフォルト：1.0長さ単位

initial_overlap

並進および円筒ジョイントの滑りパートの初期オーバーラップを指定します。

デフォルト：1000.0長さ単位

overlap_delta

滑りジョイントの摩擦特性を指定します。

INCREASE

IマーカーがJマーカーのz軸の正方向に並進すると、オーバーラップが増加します。

DECREASE

オーバーラップがJマーカーの正方向に減少します。

デフォルト：CONSTANT

yoke_choice

フックおよびユニバーサルジョイントのヨークの選択を指定します。

bristle_stiffness

LuGreモデルのブリッスル剛性σ₀を指定します。詳細については、コメント1～4をご参照ください。

デフォルト：100

damping_effects

事前に設定された変位（またはスティクション）状態の減衰係数を定義します。その主な役割は、事前に設定された変位状態でのブリッスル振動を弱めることです。このドキュメントではσ₁と表します。詳細については、コメント1～4をご参照ください。

デフォルト：0.316

viscous_effects

相対滑りが実際に始まるときに発生する粘性減衰力の係数を指定します。このドキュメントではσ₂と表します。詳細については、コメント1～4をご参照ください。LuGreモデルの非活動性（常にエネルギーを消散しているなど）を確保するには、次の状態が満たされる必要があります。

$${\sigma }_1<\frac{{\sigma }_2{\mu }_d}{{\mu }_s-{\mu }_d}$$

デフォルト：0.0004

例

<Force_JointFriction
    id                     = "1"

    joint_id               = "301001"

    mu_static              = "0.5"

    mu_dynamic             = "0.3"

    inactive               = "NONE"

    stiction_trans_vel     = "10."

    effect                 = "All"

    torque_preload         = "0."

    friction_arm           = "7."

    pin_radius             = "5."

    bending_reaction_arm   = "5."

    inputs                 = "1111"   
 />

<?xml version="1.0"?>
<?xml-stylesheet type="text/xsl"
 href="http://www.altairhyperworks.com/motionsolve-xml/motionsolve_v1.xsl"?
>
<MultiBodySystem
 xmlns:xs="http://www.w3.org/2001/XMLSchema-instance"
 xs:noNamespaceSchemaLocation="http://www.altairhyperworks.com/motionsolve-
 xml/motionsolve_v1.xsd"
  hw_version             = "11.0">
 <Messaging
     log_option          = "Overwrite"
 />
 <Model>
  <Param_Transient
     integrator_type     = "DSTIFF"
     integr_tol          = "0.0001"
     h_max               = "0.1"
     h0_max              = "0.005"
     h_min               = "1.0000E-06"
     max_order           = "6"
     vel_tol_factor      = "1000."
     rel_abs_tol_ratio   = "0.01"
     central_difference  = "FALSE"
     dae_constr_tol      = "0.000001"
     dae_corrector_maxit = "10"
     dae_corrector_minit = "0"
     dae_index           = "3"
     dae_vel_ctrl        = "TRUE"
     dae_jacob_init      = "1"
     hht_alpha           = "-0.33"
     newmark_beta        = "0.36"
     newmark_gamma       = "0.7"
  />
  <Param_Unit
     force_unit          = "NEWTON"
     mass_unit           = "KILOGRAM"
     length_unit         = "MILLIMETER"
     time_unit           = "SECOND"
  />
  <Reference_Marker
     id                  = "30101010"
     label               = "Global Frame"
     body_id             = "30101"
     body_type           = "RigidBody"
  />
  <Reference_Marker
     id                  = "30101020"
     label               = "Joint 0-Marker J"
     body_id             = "30101"
     body_type           = "RigidBody"
     a00                 = "-1."
     a10                 = "0."
     a20                 = "0."
     a02                 = "0."
     a12                 = "1."
     a22                 = "0."
  />
  <Reference_Marker
     id                  = "30102020"
     label               = "Joint 0-Marker I"
     body_id             = "30102"
     body_type           = "RigidBody"
     a00                 = "-1."
     a10                 = "0."
     a20                 = "0."
     a02                 = "0."
     a12                 = "1."
     a22                 = "0."
  />
  <Reference_Marker
     id                  = "30102030"
     label               = "bob-Marker CM"
     body_id             = "30102"
     body_type           = "RigidBody"
     pos_x               = "-100."
     pos_y               = "0."
     pos_z               = "0."
  />
  <Reference_Marker
     id                  = "73780000"
     label               = "LPRFMarker/73780000"
     body_id             = "30102"
     body_type           = "RigidBody"
  />
  <Reference_Marker
     id                  = "90000000"
     body_id             = "30102"
     body_type           = "RigidBody"
     pos_x               = "-100."
     pos_y               = "0."
     pos_z               = "0."
     a00                 = "0."
     a10                 = "1."
     a20                 = "0."
     a02                 = "1."
     a12                 = "0."
     a22                 = "0."
  />
  <Reference_Marker
     id                  = "90000001"
     body_id             = "30102"
     body_type           = "RigidBody"
     pos_x               = "-100."
     pos_y               = "0."
     pos_z               = "0."
     a00                 = "0."
     a10                 = "1."
     a20                 = "0."
     a02                 = "1."
     a12                 = "0."
     a22                 = "0."
  />
  <Reference_Marker
     id                  = "90000002"
     body_id             = "30102"
     body_type           = "RigidBody"
     a00                 = "0."
     a10                 = "-1."
     a20                 = "0."
     a02                 = "-1."
     a12                 = "0."
     a22                 = "0."
  />
  <Reference_Marker
     id                  = "90000012"
     body_id             = "30102"
     body_type           = "RigidBody"
     pos_x               = "-100."
     pos_y               = "-9.86361"
     pos_z               = "-9.86361"
  />

<Body_Rigid
     id                  = "30101"
     label               = "Ground"
     IsGround            = "TRUE"
  />
  <Body_Rigid
     id                  = "30102"
     label               = "bob"
     cg_id               = "30102030"
     im_id               = "30102030"
     lprf_id             = "73780000"
     mass                = "1."
     inertia_xx          = "1000."
     inertia_yy          = "1000."
     inertia_zz          = "1000."
  />
  <Constraint_Joint
     id                  = "301001"
     label               = "Joint 0"
     type                = "REVOLUTE"
     i_marker_id         = "30102020"
     j_marker_id         = "30101020"
  />
  <Force_Gravity
     grav_x              = "0."
     grav_y              = "0."
     grav_z              = "-9810."
  />
 <Force_JointFriction
     id                  = "1"
     joint_id            = "301001"
     mu_static           = "0.5"
     mu_dynamic          = "0.3"
     inactive            = "NONE"
     stiction_trans_vel  = "10."
     effect              = "All"
     torque_preload      = "0."
     friction_arm        = "7."
     pin_radius          = "5."
     bending_reaction_arm= "5."
     inputs              = "1111"
  />
  <Post_Request
     id                  = "1"
     comment             = "Joint omega"
     type                = "EXPRESSION"
     expr1               = "NULL"
     expr2               = "WZ(30102020,30101020,30101020)"
     expr3               = "NULL"
     expr4               = "NULL"
     expr5               = "NULL"
     expr6               = "NULL"
     expr7               = "NULL"
     expr8               = "NULL"
  />
  <Post_Request
     id                  = "2"
     comment             = "Joint friction"
     type                = "EXPRESSION"
     expr1               = "NULL"
     expr2               = "FRICTION(1,1)"
     expr3               = "FRICTION(1,2)"
     expr4               = "FRICTION(1,3)"
     expr5               = "NULL"
     expr6               = "FRICTION(1,4)"
     expr7               = "FRICTION(1,5)"
     expr8               = "FRICTION(1,6)"
  />
  <Post_Graphic
     id                  = "90000"
     type                = "Frustum"
     center_marker_id    = "90000000"
     top_radius          = "1."
     bottom_radius       = "1."
     length              = "100."
     ends_type           = "OPEN"
     refinement_level    = "2"
     is_material_inside  = "TRUE"
  />
  <Post_Graphic
     id                  = "90001"
     type                = "Frustum"
     center_marker_id    = "90000001"
     top_radius          = "0."
     bottom_radius       = "1."
     length              = "0.001"
     ends_type           = "OPEN"
     refinement_level    = "2"
     is_material_inside  = "TRUE"
  />
  <Post_Graphic
     id                  = "90002"
     type                = "Frustum"
     center_marker_id    = "90000002"
     top_radius          = "0."
     bottom_radius       = "1."
     length              = "0.001"
     ends_type           = "OPEN"
     refinement_level    = "2"
     is_material_inside  = "TRUE"
  />
  <Post_Graphic
     id                  = "90012"
     type                = "BoxDefinedFromCorner"
     corner_marker_id    = "90000012"
     length_x            = "20."
     length_y            = "20."
     length_z            = "19.86361"
     is_material_inside  = "TRUE"
  />
 </Model>
 <Command
     time_out            = "999999"> <!--In SECONDS-->
  <H3DOutput
     switch_on           = "TRUE"
  />
  <ResOutput
     plt_file            = "TRUE"
  />
  <Simulate
     analysis_type       = "Transient"
     end_time            = "5."
     num_step            = "1000"
  />
 </Command>
</MultiBodySystem>

コメント

1. MotionSolveは、摩擦にLuGre（Lundt-Grenoble）モデルを使用します。このモデルの概要は以下のとおりです：
   摩擦の理想化にはブリッスルモデルが使用されます。摩擦は、2つのあわせ面の間の弾性スプリングの平均たわみ力としてモデル化されます。接線方向のモーションが適用されると、ブリッスルはスプリングのようにたわみます。たわみが十分大きくなると、ブリッスルは滑り始めます。あわせ面間の滑り速度v_slipにより、定常モーションでの平均ブリッスルたわみが決まります。これは速度が遅いと大きくなり、速度が上がると定常たわみは小さくなることを意味します。 図 2 に、ブリッスルモデルを示します。

   
   
   

2. LuGreモデルは、いくつかの異なる効果を表すことができます：
   • あわせ面が潤滑剤によって押し分けられる効果。
   • ストライベック効果（非常に低速の場合）。部分的に流体の潤滑剤が存在する場合、あわせ面間の接触が減少し、これによりスティクションの状態から摩擦が指数関数的に減少します。
   • 2つのあわせ面間のさまざまな離反力や静摩擦の遅延など、速度依存の摩擦現象。
3. １次元の摩擦の場合、LuGreモデルは次のように表されます。

   $F=LuGre({\mu }_s,{\mu }_d,\sigma ,N,v,z)$ $F=N({\sigma }_{0}z+{\sigma }_1\frac{dz}{dt})+{\sigma }_{2}v$ $\sigma =\left[{\sigma }_0{\sigma }_1{\sigma }_2\right]$ $g(v)={\mu }_d+\left({\mu }_s-u_d\right)e^{-{(\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$vs$}\right.)}^2}$ $\frac{dz}{dt}=v-{\sigma }_0\frac{\left|v\right|z}{g(v)}$

   状態 z = ブリッスルたわみ 入力 v = 滑り速度 vs = 静摩擦から動摩擦への遷移滑り速度 パラメータ s0 = ブリッスル剛性 s1 = 減衰係数 s2 = 粘性係数 vs = スティクション遷移速度 出力 F = 摩擦力

4. LuGre関数は次のように表されます：関数g(v)は、摩擦関数の形状を定義します。

   
   
   

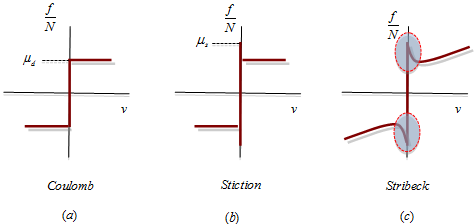
   図 3に示すように、g(v)は、クーロン摩擦(a)、スティクション(b)、およびストライベック効果(c)をモデル化できます。その定義より、 ${\mu }_d\le g(v)\le {\mu }_s$ となります。

   ごく細かいレベルで、2つのあわせ面はさまざまなざらついた部分で接触しています。このようなざらつきがブリッスルで表され、2つのあわせ面の間の相対速度が存在する場合、このブリッスルがスプリングのようにたわみます。スプリングのたわみにより、摩擦力が生じます。たわみが十分な大きさである場合、表面が不規則なため、ブリッスルは非常にランダムに滑ります。ブリッスルのたわみはランダムですが、LuGreモデルでは平均たわみのみを考慮します。ブリッスルの平均たわみzは、ブリッスルのたわみを滑り速度、摩擦係数、および垂直抗力と関連付ける1次微分方程式でモデル化されます。

   • パラメータσ₀はブリッスル剛性を表します。これは摩擦要素における微小変形に抵抗する剛性をモデル化するものです。
   • パラメータσ₁は、事前に設定された変位（またはスティクション）状態での減衰を表します。摩擦の状態がこの状態からかけ離れている場合、この影響は無視できます。すべり速度vがゼロに近い事前設定された変位のゾーンからシステムが離れると、この速度vより速い時間スケールでは、 $\dot{z}$ はゼロになる傾向があるためです。
   • パラメータσ₂は、粘性減衰を表します。これは、滑り速度vが増加すると摩擦力が増加する主要因となります。2つのあわせ面間に滑り速度が存在する場合、粘性効果によって減衰が決まります。
5. LuGreモデルでは、図 4に示すようなヒステリシスを捉えることができます。

   
   
   

6. LuGreモデルでは、図 5に示すような周波数依存のヒステリシスも捉えることができます。

   
   
   

7. LuGreモデルを使用して、次のようにN次元での摩擦を表すこともできます。関連する3D空間を以下のとおりとします。
   • 滑り速度 $v_r={\left[v_x{v}_y{v}_z\right]}^T$ 、 $v_m=\Vert v_r\Vert$
   • ブリッスル状態 $Z_r={\left[Z_x{Z}_y{Z}_z\right]}^T$
   ここで次の項を定義します：

   • $g(v_m)={\mu }_d+\left({\mu }_s-u_d\right)e^{-{(\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$vs$}\right.)}^2}$
   3D LuGre摩擦モデルは、以下の式で定義されます：

   • $\frac{d{z}_i}{dt}=v_i-{\sigma }_0\frac{\left|v_m\right|z_i}{g(v_m)}$
   • $F_{x,y,z}=LuGre3d({\mu }_s,{\mu }_d,\sigma ,N,v,z)$ 、 $F_i=N({\sigma }_0{z}_i+{\sigma }_1\frac{d{z}_i}{dt})+{\sigma }_2{v}_i$
   • i=x,y,z
8. 摩擦力結合。

   結合効果により、図 6に示すように、x、y、z方向に滑りが見られる場合に、制動力を定義するなじみのある摩擦楕円が導かれます。

   
   
   

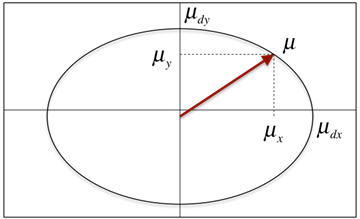
9. 回転ジョイントにおける摩擦。

   図 7 は、回転ジョイントの形状を表しています。灰色で示した円形ピンは、2つのボディ（1と2）を保持し、これらが図の平面に垂直なz軸を中心に回転できるようにしています。挿入図は、ピンを通るジョイントのyz断面を示しています。

   
   
   

   次の形状プロパティは摩擦の計算にとって重要です：

   • ピンの半径、r_p。
   • 曲げ反動アーム、r_b。内側のパートPart-1の幅は、2*r_bです。
   • 摩擦アーム、r_n。これは、軸力が作用する有効半径です。
   マルチボディシミュレーションでは、いくつかの方法で荷重をジョイントに適用し、反力および反トルクを生成できます。これらはそれぞれ、摩擦力によって界面動力学に寄与します。回転ジョイントの場合、寄与する効果が4つあります：

   • xy平面の垂直抗力Nxyによって生じるピンの円筒サーフェス上の摩擦。
   • 軸力Nzによって生じるピンのエンドキャップ上の摩擦。
   • xy平面のモーメントアームと等価な偶力Nrxyによって生じる摩擦。
   • ジョイントのアセンブリプリロードによって生じる摩擦。
   これらの各効果の計算について以下に説明します。

   xy平面の垂直抗力N_xyによって生じるピンの円筒サーフェス上の摩擦。

   図 8の(a)は、xy平面の荷重により生じる寄与について示しています。接触サーフェスはピンに位置するため、滑り速度はピンの半径とジョイントの相対角速度ω_rに依存します。

   xy平面の滑り速度は、v_slip1=ω_rr_pとなります。

   ピンサーフェスに垂直な力は、 $N_{xy}=\sqrt{\left(N_x^2+N_v^2\right)}$ となります。

   摩擦力は、 $F_{xy1}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_{xy},v_{slip1},z)$ となります。

   この摩擦力によって生成されるトルクは、T_z1=F_x1r_pとなります。

   
   
   

   軸力N_zによって生じるピンのエンドキャップ上の摩擦。

   図 8の(b)から、軸荷重による摩擦で、有効半径r_nの円環板状の接触サーフェスが生じることがわかります。したがって、軸方向の滑り速度は、v_slip1=ω_rr_nとなります。ピンサーフェスに垂直な力は、N_zです。

   軸荷重に対する摩擦力の大きさは、 $F_{xy2}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_z,v_{slip2},z)$ となります。

   軸荷重による摩擦トルクは、T_z2=F_xy2r_nとなります。

   xy平面のモーメントアームと等価な偶力N_rxyによって生じる摩擦。

   反モーメントは、さらに摩擦トルクを生じさせることもあります。これを図 9に示します。

   
   
   

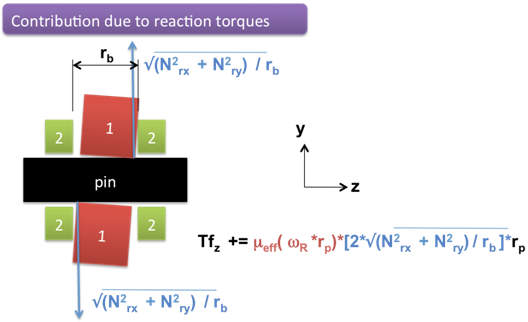
   この場合、まず、反トルクから得られる個々の反作用を特定する必要があります。図 7に基づき、反モーメントのモーメントアームがr_bなので、偶力は次のようになります：

   $N_{rxy}=\frac{\sqrt{\left(N_{rx}^2+N_{ry}^2\right)}}{r_b};N_{rxy}$ は、接触サーフェスに作用する反力です。

   垂直抗力が半径r_pで作用します。したがって、摩擦力は次のように表すことができます：

   $F_{rxy}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_{rxy},{\omega }_p{r}_p,z)$ .

   この摩擦力によって生じる摩擦トルクは、T_z3=F_rxyr_pとなります。

   ジョイントのアセンブリプリロードによって生じる摩擦

   トルクのプリロードは、μ_sで除算され、ピンの円筒サーフェスに垂直な等価な力が算出されます。次に、サーフェス上の摩擦力が、LuGre関数を使用して計算されます。最後に、円筒サーフェス上の摩擦力が、その摩擦力のモーメントを計算することで求められます。

   $N{}_{preload}=F_{preload}/\left({\mu }_s{r}_p\right)$

   $F_{preload}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_{preload},{\omega }_p{r}_p,z)$

   T_z4=F_preloadr_p

   プリロードによる摩擦力は、T_z4となります。

   回転ジョイントの合計摩擦トルクは、T_Jfric=T_z1+T_z2+T_z3+T_z4となります。

10. 並進ジョイントにおける摩擦。

    図 10 は、並進ジョイントの形状を表しています。黒色で示された長方形のスロットのスライダーが、青色で示された直方体のボディ上をスライドします。青色のボディ上のマーカーJのz軸が、並進の軸となります。挿入図は、スライダーを通るジョイントのxy断面を示しています。

    
    
    

    次の形状プロパティは摩擦の計算にとって重要です：

    • 反動アーム、r_n。
    • 並進軸に沿ったスライダーのサイズ、x_s0。
    いくつかの方法で荷重を並進ジョイントに適用することができ、それぞれで摩擦力が生じます。合計摩擦力は、これらの各効果の合計です。並進ジョイントの場合、寄与する効果が4つあります：

    • 図 11(a)のスライダーと接するブロックがこすれることによって生じるxy平面の摩擦。
    • 図 11(b)のスライダーと接するブロックがねじれることによって生じるxy平面の摩擦。
    • 図 11(c)のスライダーが曲げられることによって生じるyz平面の摩擦。
    • ジョイントのアセンブリプリロードによって生じる摩擦。

    
    
    

    スライダーと接するブロックがこすれることによる、xy平面の摩擦

    xy平面に作用する垂直抗力を図 10(a)に示します。N_xおよびN_yは、それぞれxおよびy方向の、ブロックとスライダー間の相対運動を妨げる拘束力です。

    したがって垂直抗力は、 $N=\sqrt{\left(N_x^2+N_y^2\right)}$ となります。

    軸荷重に対する摩擦力の大きさは、 $=F_{z1}=LuGre({\mu }_s,{\mu }_d,\sigma ,N,v_z,z)$ となります。

    スライダーと接するブロックがねじれることによる、xy平面の摩擦

    図 10(b)を参照すると、ブロックとスライダー間のねじりモーメントにより、ブロックの2つの角で接触が生じています。接触ポイント間の距離をr_nで一定と見なすと、ねじりモーメントN_rzは、各接触ポイントで作用する、同じ大きさで反対向きの偶力N_xyに置き換えることができます。

    $N_{xy}=\frac{N_{rz}}{2_{rn}}$

    ねじりによる摩擦力は、 $=F_{z2}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_{xv},v_z,z)$ となります。

    スライダーが曲げられることによる、xzおよびyz平面の摩擦

    図 10(c)を参照すると、曲げモーメントは、スライダーに対してブロックを曲げる傾向があります。initial_overlapとoverlap_deltaの関数で表される距離だけ離れた2点で、接触が生じます。これらの接触間の距離をx_sとします。曲げモーメントをモーメントアームx_sの偶力で置き換えると次のようになります：

    $$N_{xy3}=\frac{\sqrt{\left(N_{rx}^2+N_{ry}^2\right)}}{x_s}$$

    曲げによる摩擦力は、 $=F_{z3}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_{xy3},v_z,z)$ となります。

    ジョイントのアセンブリプリロードによって生じる摩擦

    力のプリロードは、μ_sで除算され、ジョイントの接触サーフェスに垂直な等価な力が算出されます。次に、サーフェス上の摩擦力が、LuGre関数を使用して計算されます。したがって次のようになります：

    $$N_{preload}=\raisebox{1ex}{$T_{preload}$}\!\left/ \!\raisebox{-1ex}{${\mu }_s$}\right.$$

    プリロードによる摩擦力は、 $=F_{z4}=LuGre({\mu }_s,{\mu }_d,\sigma ,N_{preload},v_z,z)$ となります。

    並進ジョイントの合計摩擦力は、F_Jfric=F_z1+F_z2+F_z3+F_z4となります。

11. 円筒ジョイントにおける摩擦。

    図 12 は、円筒ジョイントの形状を表しています。灰色で示された円形のスロットのスライダーが、青色で示された円形シャフト上をスライドします。青色のシャフト上のマーカーJのz軸が、並進および回転の軸となります。挿入図は、スライダーを通るジョイントのxy断面を示しています。

    次の形状プロパティは摩擦の計算にとって重要です：

    • ピン半径、r_n。
    • 並進軸に沿った曲げモーメントアーム、x₀。

    
    
    

    いくつかの方法で荷重を円筒ジョイントに適用することができ、それぞれで摩擦力が生じます。合計摩擦力は、これらの各効果の合計です。円筒ジョイントの場合、寄与する効果が3つあります：

    • 図 12(a)のラジアル荷重によって生じる摩擦力 / トルク。
    • 図 12(b)のスライダーが曲げられることによる摩擦力 / トルク。
    • ジョイントのアセンブリプリロードによって生じる摩擦力 / トルク。

    
    
    

    ラジアル荷重によって生じる摩擦力 / トルク

    xy平面に作用する垂直抗力を図 13(a)に示します。N_xおよびN_yは、それぞれxおよびy方向の、ブロックとスライダー間の相対運動を妨げる拘束力です。

    従って垂直抗力は、 $N=\sqrt{\left(N_x^2+N_y^2\right)}$ 、接触ポイントでの滑り速度は、 $v={\left[\omega r_{p}0v_z\right]}^T$ となります。

    ブリッスルたわみ $Z={\left[Z_{rot}0Z_{trans}\right]}^T$ を定義します。

    ラジアル荷重による摩擦力は、 $F_{zy1,0z1}=LuGre3d({\mu }_s,{\mu }_d,\sigma ,N,v_z,z)$ となります。

    ラジアル荷重による摩擦トルクは、 $=T_{z1}=r_p\cdot F_{xy1}$ となります。

    スライダーが曲げられることによる摩擦力 / トルク

    図 11(b)を参照すると、曲げモーメントは、スライダーに対してブロックを曲げる傾向があります。initial_overlapとoverlap_deltaの関数で表される距離だけ離れた2点で、接触が生じます。これらの接触間の距離をx_sとします。曲げモーメントをモーメントアームx_sの偶力で置き換えると次のようになります：

    $$N_{xy2}=\frac{\sqrt{\left(N_{rx}^2+N_{ry}^2\right)}}{x_s}$$

    曲げによる摩擦力は、 $F_{xy2,0z2}=LuGre3d({\mu }_s,{\mu }_d,\sigma ,N,v,z)$ となります。

    曲げによる摩擦トルクは、 $=T_{z2}=r_p\cdot F_{xy2}$ となります。

    ジョイントのアセンブリプリロードによって生じる摩擦力 / トルク

    力のプリロードは、μ_sで除算され、ジョイントの接触サーフェスに垂直な等価な力が算出されます。次に、サーフェス上の摩擦力が、LuGre関数を使用して計算されます。したがって次のようになります：

    $$N_{preload}=\raisebox{1ex}{$F_{preload}$}\!\left/ \!\raisebox{-1ex}{${\mu }_s$}\right.$$

    プリロードによる摩擦力は、 $F_{xy3,0z3}=LuGre3d({\mu }_s,{\mu }_d,\sigma ,N_{preload},v,z)$ となります。

    プリロードによる摩擦トルクは、 $=T_{z3}=r_p\cdot F_{xy3}$ となります。

    円筒ジョイントの円周の合計摩擦力は、=F_xy1+F_xy2+F_xy3=0となります。

    円筒ジョイントの合計軸摩擦力は、F_Jfric=F_z1+F_z2+F_z3となります。

    円筒ジョイントの合計摩擦トルクは、=T_Jfric=T_z1+T_z2+T_z3となります。

12. ユニバーサルジョイントにおける摩擦。

    ユニバーサルジョイントは、概念的に、2つの回転ジョイントで構成されたものと考えることができます。1つの回転ジョイントの軸はI-Yokeに沿っており、もう1つの回転ジョイントの軸はJ-Yokeに沿っています。各ヨークでの摩擦は、回転ジョイントと同様にモデル化されます。回転ジョイントの摩擦のモデル化の詳細については、コメント8をご参照ください。

13. 球ジョイントにおける摩擦。
    球ジョイントでは、3つすべての軸の周りの回転が可能で、すべての並進自由度が拘束されます。したがって、球ジョイントに関する力学は、ボールの球面上の相対運動にあてはめることができます。球ジョイントの一般的な荷重シナリオを図 13に示します。この場合、以下の図 14より、摩擦の計算には次の形状プロパティが重要です：

    • ボール半径、r_b。

      ボールとソケット間の拘束力、およびジョイントのアセンブリプリロードにより、荷重を球ジョイントに適用することができます。合計摩擦力は、これらの各効果の合計です。簡素化のため、垂直抗力をジョイントの反力とプリロード力の合計として定義します。これは、下の図で $\overrightarrow{N}$ と表されています。

      次のように定義します： $N=\Vert \overrightarrow{N}\Vert$

      ソケットに対するボールの角速度は、 ${\omega }_r=\left[{\omega }_x{\omega }_y{\omega }_z\right]$ となります。

      
      
      

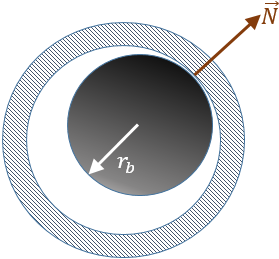
      滑り速度の成分は、全体座標系で次のように計算できます：

      滑り速度 $v_r={\left[r_b{\omega }_x{r}_b{\omega }_y{r}_b{\omega }_z\right]}^T$ 、 $v_m=\Vert v_r\Vert$ ブリッスル状態 $Z={\left[Z_x{Z}_y{Z}_z\right]}^T$

      コメント6で説明した規則に従って、球ジョイントの摩擦力は、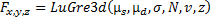となります。

      そして摩擦トルクは、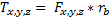となります。

14. フックジョイントにおける摩擦。

    フックジョイントは、概念的に、2つの回転ジョイントで構成されたものと考えることができます。1つの回転ジョイントの軸はI-Yokeに沿っており、もう1つの回転ジョイントの軸はJ-Yokeに沿っています。各ヨークでの摩擦は、回転ジョイントと同様にモデル化されます。回転ジョイントの摩擦のモデル化の詳細については、コメント8をご参照ください。

15. 参照：
    • C. Canudas de Wit、H. Olsson、K. J. Aström、およびP. Lischinsky、A New Model for Control of Systems with Friction。IEEE Transactions on Automatic Control、1995年3月、vol.40、No.3、419-425ページ。
    • Velenis E.、Tsiotras P.、Canudas-de-Wit C.(2005)、“Extension of the LuGre Dynamic Tire Friction Model to 2D Motion”、Vehicle System Dynamics、2005年。
    • Bliman、P. A. Sorine, M.、“Friction modeling by hysteresis operators.Application to Dahl, sticktion and Stribeck effects”、Pitman Research Notes in Mathematics Series、1993年、Issue 286、10ページ。
    • Olsson, H、Aström, K. J、Canudas De Wit, C、Gaefvert, M、Lischinsky, P、“Friction Models and Friction Compensation”、European Journal of Control、1998年、Vol. 4、Number 3、176-195ページ。
    • J. C. Trinkle、J.-S. Pang、S. Sudarsky、G. Lo、“On Dynamic Multi-Rigid-Body Contact Problems with Coulomb Friction”、ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik、Volume 77、Issue 4、267-279ページ、1997年。