Point Mass

Model ElementBody_Point defines a point mass entity in MotionSolve.

Description

This entity has mass, but no inertia properties. The position of a point mass is characterized by three translational coordinates. By default, the orientation of the point mass is set to be the same as the global coordinate system. It never changes during simulation.

Reference_Markers on Body_Point may have location and orientation coordinates. The orientation of these Reference_Markers does not change during the simulation.

Format

<Body_Point
     id                  = "integer"   
[    label               = "string" ]     
     cg_id               = "integer"   
[    lprf_id             = "integer" ]     
     mass                = "real"     
     v_ic_x              = "real"     
     v_ic_y              = "real"     
     v_ic_z              = "real"     
     v_ic_x_flag         = { "TRUE" | "FALSE" }     
     v_ic_y_flag         = { "TRUE" | "FALSE" }     
     v_ic_z_flag         = { "TRUE" | "FALSE" }
</Body_Point>

Attributes

id
Element identification number, (integer>0). This number is unique among all Body_Point elements.
label
The name of the Body_Point element.
cg_id
Specifies the Reference_Marker that is located at the center-of-mass of the Body_Point.
lprf_id (optional)
Specifies the local part reference marker.
mass
Specifies the mass of the Body_Point. Mass > 0.
v_ic_x
Specifies the initial translational velocities of the Body_Point CG Reference_Marker along the global x-axis.
v_ic_y
Specifies the initial translational velocities of the Body_Point CG Reference_Marker along the global y-axis.
v_ic_z
Specifies the initial translational velocities of the Body_Point CG Reference_Marker along the global z-axis.
v_ic_x_flag
A Boolean flag that indicates whether the x-velocity is known exactly or is just an initial guess.
"TRUE" means this initial condition is applied exactly unless it is in conflict with a Motion input.

"FALSE" means this initial condition is applied as an initial guess. It may be changed by MotionSolve to ensure that all constraints are satisfied.

v_ic_y_flag
A Boolean flag that indicates whether the y-velocity is known exactly or is just an initial guess.
"TRUE" means this initial condition is applied exactly unless it is in conflict with a Motion input.
"FALSE" means this initial condition is applied as an initial guess. It may be changed by MotionSolve to ensure that all constraints are satisfied.
v_ic_z_flag
A Boolean flag that indicates whether the z-velocity is known exactly or is just an initial guess.
"TRUE" means this initial condition is applied exactly unless it is in conflict with a Motion input.
"FALSE" means this initial condition is applied as an initial guess. It may be changed by MotionSolve to ensure that all constraints are satisfied.

Example

The three body problem is one of the oldest problems in dynamical systems. The problem is to determine the behavior of three interacting celestial masses, for example the Earth, Moon and Sun. No closed form solutions have been found for the general problem and numerical simulations are performed to predict the behavior of the three bodies. The scale of the system is such that the three bodies can be considered as point masses.

Mass:
  • The mass of the Sun is 1.988 × 1030 kg.
  • The mass of the Earth is 5.974 × 1024 kg.
  • The mass of the moon is 7.475 × 1022 kg.
Choose the mass of the Earth as the mass unit; then:
  • The mass of the Sun is 3.328E+5.
  • The mass of the Earth is 1.000.
  • The mass of the moon is 1.251E-2.
Distance:
  • The distance from the Sun to the Earth is 1.496 x 108 km.
  • The distance from the Moon to the Earth is 3.844 x 105 km.
Choose the mean distance from the Earth to the Moon as the distance unit; then:
  • The distance from the Sun to the Earth is 389.2.
  • The distance from the Moon to the Earth is 1.000.
Time:
  • The time unit is set to 1 year (365 days), so a long term simulation can be performed.
Initial velocities:
  • The velocity of the Earth with respect to the Sun is 29.8 Km/s. This is equivalent to 2.445 x 103 Moon-Earth distances per year.
  • The velocity of the Moon with respect to the Earth is 3680 km/hr. This is equivalent to 83.86 Moon-Earth distances per year.

The global coordinate system is placed at the CG of the Sun. At the start of the simulation, the Earth is assumed to be along the X-axis of the global coordinate system. The moon is assumed to be in the X-Y plane as shown in the figure below.

Figure 1. The Sun-Earth-Moon System


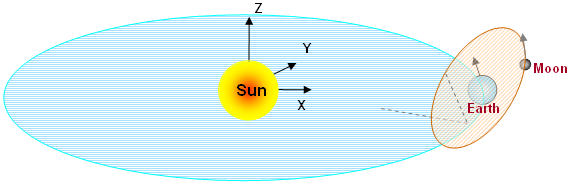
The Body_Point defining the sun in this system of units would be:

<Body_Point
     id                  = "1"
     cg_id               = "11"
     mass                = "3.328E+5"
     v_ic_x              = "0.0"
     v_ic_y              = "0.0"
     v_ic_z              = "0.0"
     v_ic_x_flag         = "TRUE"
     v_ic_y_flag         = "TRUE"
     v_ic_z_flag         = "TRUE"
</Body_Point>

The Body_Point defining the Earth in this system of units would be:

<Body_Point
     id                  = "2"
     cg_id               = "21"
     mass                = "1.0"
     v_ic_x              = "0.0"
     v_ic_y              = "2.445E+3"
     v_ic_z              = "0.0"
     v_ic_x_flag         = "TRUE"
     v_ic_y_flag         = "TRUE"
     v_ic_z_flag         = "TRUE"
    </Body_Point>

Comments

  1. A point mass in physics is an idealization of a body whose dimensions are very small compared to the other distances which are relevant to the problem. In such cases, the internal structure of the body can be neglected, and the body can be treated as if its mass were concentrated at one point in space.

    In some situations, the body can be treated as a point mass for some purposes even if its dimensions are not negligibly small. For example, the gravitational field outside a spherically-symmetric body is the same as if the body were a point mass positioned at the center (with the same total mass, acting as a point source of gravitation).

  2. Body_Point can be connected with the other bodies (point, flexible or rigid) with constraint and force elements. Any torque applied to Body_Point is ignored since it has no effect on the motion of the Body_Point .
  3. All constraint elements are supported. A few force elements are not supported. These are: Force_Beam and Force_Field.