HS-1630： Fluxの応用例をベースとしたOptimization（最適化）の設定

本チュートリアルでは、金型プレスモデルのOptimization（最適化）を行い、半径方向を向いた磁石を得ます。

チュートリアルを始める前に：
  • 本チュートリアルで使用されるFluxファイル群を<hst.zip>/HS-1630/から自身の作業ディレクトリにコピーします。
  • HyperStudyと連成されるようFluxをセットアップします。詳細については、Fluxモデルの登録手順をご参照ください。

このチュートリアルは、金型プレスモデルの最適化に特化した例TEAM 25をベースとしています。

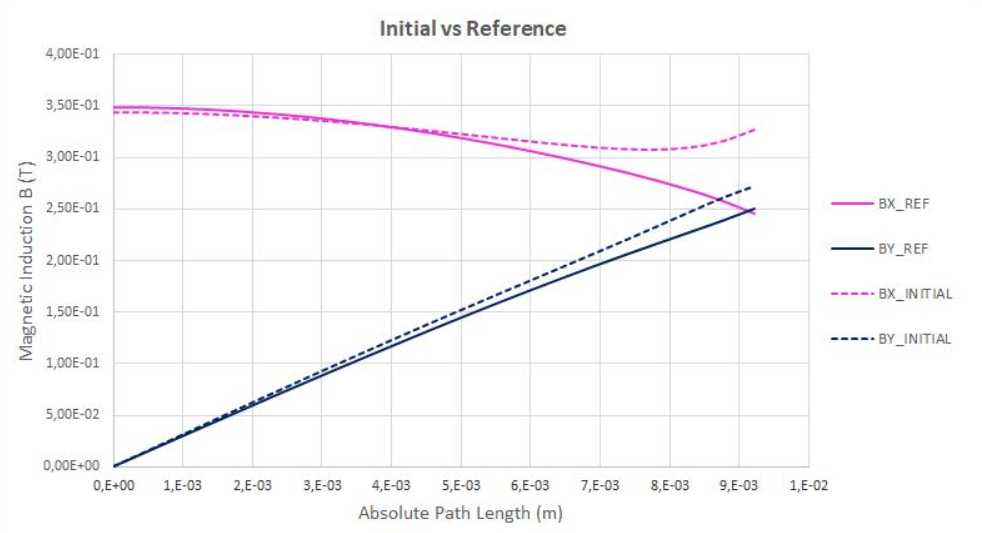
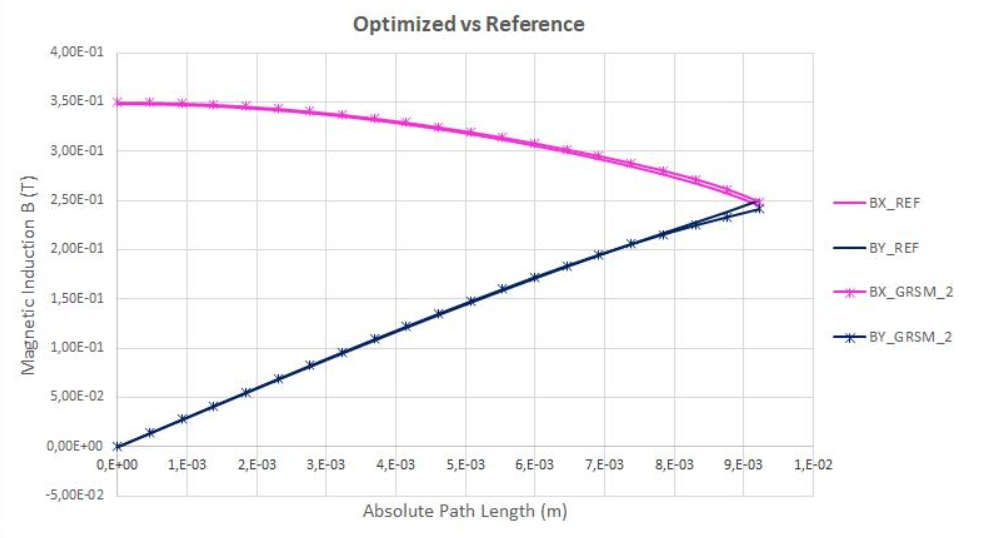
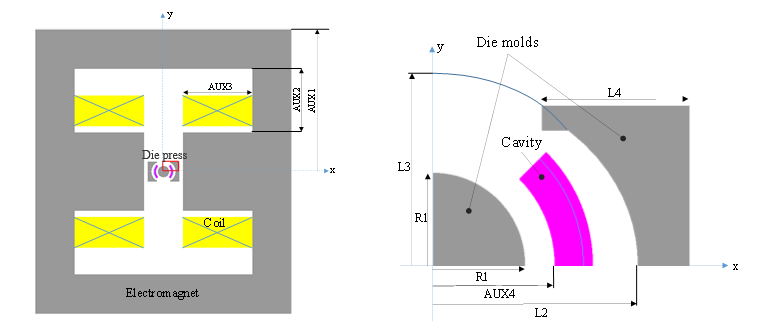
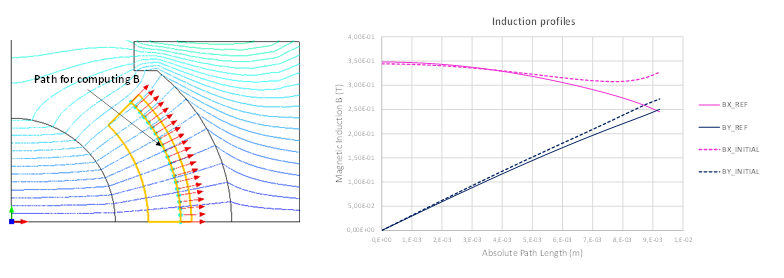
下の図は、Flux 2Dでモデル化された金型モデルでの電磁石を中央に示しています。金型モデルは、空間内に放射状の流れの分散を生じるようセットされています。目的は、空間内に挿入された磁石上に特有の磁気誘導 Β → MathType@MTEF@5@5@+= feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaacq qHsoGqaiaawEniaaaa@3909@ を得ることにあります： Β x MathType@MTEF@5@5@+= feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuOKdiKaam iEaaaa@3852@ ここで、計算パスに沿った Β y MathType@MTEF@5@5@+= feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuOKdiKaam yEaaaa@3853@ は、下の図に示すリファレンスに適合しなければなりません。下の図は、8個の設計とそれらのばらつきの範囲を示しています。

図 1.


表 1.
パラメータ Initial (mm) Min (mm) Max (mm)
R1 7.2 5 9.4
L2 15.3 12.6 18
L3 14 14 45
L4 11.5 4 19
AUX1 180 170 190
AUX2 80 70 90
AUX3 88 86 90
AUX4 9.5 9.5 11
図 2.


この種の最適化問題を解くのに最良な方法は、各ポイントにおける計算値と参照値との間の二乗差の合計の積分を最小化することです。目的関数は下の式で定義されます。ここで、nは計算パス上のポイントの数です。
図 3.
F = ∑ i = 1 n ( Β x − Β x _ r e f ) 2 + ( Β y − Β y _ r e f ) 2 MathType@MTEF@5@5@+= feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraiabg2 da9maaqahabaWaamWaaeaacaGGOaGaeuOKdiKaamiEaiabgkHiTiab fk5acjaadIhacaGGFbGaamOCaiaadwgacaWGMbGaaiykamaaCaaale qabaGaaGOmaaaakiabgUcaRiaacIcacqqHsoGqcaWG5bGaeyOeI0Ia euOKdiKaamyEaiaac+facaWGYbGaamyzaiaadAgacaGGPaWaaWbaaS qabeaacaaIYaaaaaGccaGLBbGaayzxaaaaleaacaWGPbGaeyypa0Ja aGymaaqaaiaad6gaa0GaeyyeIuoaaaa@57CA@

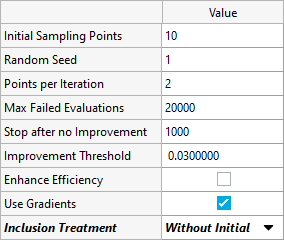
スタディのセットアップの実行

このステップでは、スタディのセットアップを行います。

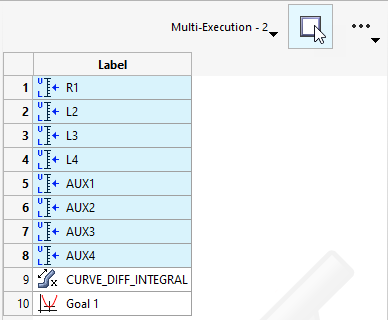
設計変数と応答はFluxで作成され、リンクファイルを介してHyperStudyにエクスポートされます。

  1. HyperStudyを開始します。
  2. 以下の方法で新規スタディを開始します：
    • メニューバーから、File（ファイル） > New（新規）をクリックします。
    • リボン上でをクリックします。
  3. Add Study（スタディの追加）ダイアログでスタディの名前を入力し、スタディの場所を選んでOKをクリックします。
    ヒント: Fluxファイル群と同じ場所にスタディを保存することが推奨されます。
  4. Define Models（モデルの定義）ステップに進みます。
    1. Directory（ディレクトリ）から、4HST.F2HSTファイルをワークエリアにドラッグ＆ドロップします。
      図 4.


    2. Import Variables（変数のインポート）をクリックします。
    HyperStudyはFluxモデルを生成し、Fluxファイルから8個の入力変数と1個の応答をインポートし、Solver Execution Script（ソルバー実行スクリプト）タブとSolver Input Arguments（ソルバー引数）タブに入力します。
  5. Define Input Variables（入力変数の定義）ステップに進みます。
    1. 下の一覧に示されるように、下限と上限の範囲を修正します。
      表 2.
      ラベル 新しい下限 新しい上限
      R1 5 9.4
      L2 12.6 18
      L3 14 45
      L4 4 19
      AUX1 170 190
      AUX2 70 90
      AUX3 86 90
      AUX4 9.5 11
  6. Test Models（モデルをテスト）ステップに進みます。
    1. Run Definition（計算実行）をクリックします。
  7. Define Output Responses（出力応答の定義）パネルに進みます。
    1. Objectives/Constraints - Goals（目的 / 制約条件 - 目標）タブをクリックし、Add Goal（目標を追加）を選択します。
    2. 目標がCurve_DIFF_INTEGRAL (r_1)について適用され、タイプがMinimize（最小化）にセットされていることを確認します。
      図 5.


    3. Evaluate（評価）をクリックします。

    スタディのディレクトリ内に、approach/nom_1/ディレクトリが作成されます。このディレクトリには、解析されたFluxファイル群が保管されているrun__00001/m_1ディレクトリが含まれています。

GRSMを使ったOptimization（最適化）の実行

ここでは、Optimization（最適化）を追加し、Global Response Search Method（大域的応答曲面法）（GRSM）法を使って実行します。

  1. Optimization（最適化）を追加します。
    1. Explorer（エクスプローラ）内で右クリックし、コンテキストメニューからAdd（追加）を選択します。
    2. Add（追加）ダイアログでOptimization（最適化）を選択し、ラベルにGRSMと入力します。
    3. Definition from（定義元）に、アプローチを選択します。
    4. OKをクリックします。
  2. Specifications（スタディ仕様）ステップに進みます。
    1. ワークエリアで、Global Response Search Method（大域的応答曲面法）（GRSM）を選択します。
    2. デフォルトの設定を保持します。
    3. 適用（適用）をクリックします。
  3. Evaluate（評価）ステップに進みます。
    1. Evaluate Tasks（計算実行）をクリックします。
      ヒント: Optimization（最適化）の進捗と最終結果は、Iteration History（反復計算履歴）タブとIteration Plot（反復計算プロット）タブで監視できます。最適解は一覧内において緑色でハイライト表示されます。
  4. オプション: 設計変数の変化vs.反復計算のプロットを表示させます。
    1. Iteration Plot（反復計算プロット）タブに進みます。
    2. Channel（チャンネル）セレクターで、R1からAUX4までのプロットを表示させます。
    3. Multiplot（マルチプロット）を選択します。
      図 6.


    4. Options（オプション）をクリックし、ドロップダウンメニューからBounds（境界）を選択します。
    5. プロットのうちの1つを右クリックし、コンテキストメニューからAll（すべて） > Legend（レジェンド）を選択します。
    6. プロットを解析し、許容される境界に達しているかを見極めます。下の図に示されるように、L3のみ下限値に達しています。
    図 7.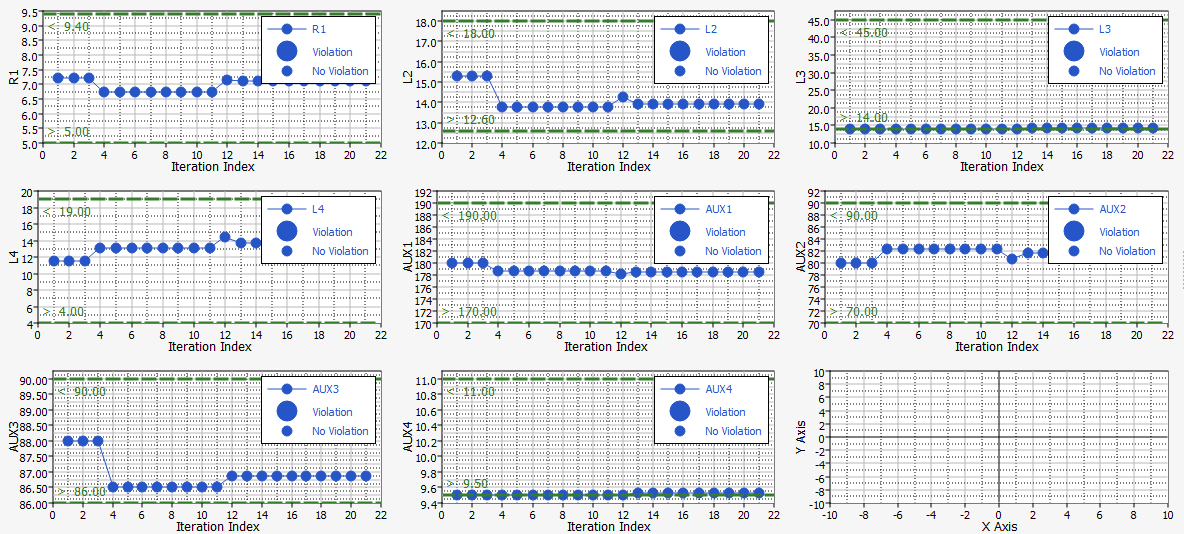


GRSMでInclusion Matrix（包含マトリックス）を使ってOptimization（最適化）を実行

ここでは、2番目のOptimization（最適化）をGlobal Response Search Method（大域的応答曲面法）（GRSM）でInclusion Matrix（包含マトリックス）を使って実行し、より良い解が得られるかを見ます。

2番目のGRSMは、GRSMを使ったOptimization（最適化）の実行での最初のOptimization（最適化）実行で求められた最適解から開始します。GRSMによる最初のOptimization（最適化）はInclusion Matrix（包含マトリックス）としてインポートされ、新たな50回の実行が完了されます。

  1. Explorer（エクスプローラ）でGRSM Optimization（最適化）アプローチを右クリックし、コンテキストメニューからCopy（コピー）をクリックします。
  2. Copy（コピー）ダイアログで、ラベルにGRSM_InclMatrixと入力し、OKをクリックします。
  3. GRSM InclMatrix > Specifications（スタディ仕様）ステップに進みます。
    1. Channel（チャンネル）セレクターで、More（その他）タブをクリックします。
    2. Use Inclusion Treatmentで、ドロップダウンメニューからWithout Initial（初期値なし）を選択し、包含マトリックスの使用を有効にします。
      図 8.


    3. Matrixエリアで、Display列のEditをクリックします。
      図 9.


    4. Edit Inclusion Matrix（包含マトリックスの編集）ダイアログで、Import Values（値のインポート）をクリックします。
    5. 一覧内でApproach evaluation data（アプローチ評価データ）を選択し、Next（次）をクリックします。
    6. ドロップダウンメニューからGRSM (opt_1)を選択しNextをクリックします。
    7. Finish（終了）をクリックし、さらにOKをクリックします。
    8. 適用（適用）をクリックしてスタディの仕様を検証します。
  4. Evaluate（評価）ステップに進みます。
    1. Evaluate Tasks（計算実行）をクリックします。

      最初のGRSMから包含された50回のランを確認できます。包含されたランは、2番目のGRSM最適化の最初の反復計算を実行するために使用されます。結果として、反復計算1の最良の解は、最初のGRSMで得られた最適解です。

結果の概要

チュートリアルの結果を確認します。

図 10.


図 11.