/MAT/LAW124 (CDPM2)

Blockフォーマットキーワード塑性、損傷、ひずみ速度効果を考慮したコンクリート材料則。

引張によるメッシュサイズ依存を避けるために、Hillerborg正則化法も利用できます。使用しやすいよう、この材料則は少ないパラメータで設定することができます。

注: この材料は現時点ではベータリリース状態であり、開発は継続中です。

フォーマット


(1)	(3)	(5)	(6)	(7)	(8)	(9)	(10)
/MAT/LAW124/`mat_ID`/`unit_ID`またはMAT/CDPM2/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$ν$		`IDEL`		`IRATE`	`FCUT`
`ECC`	$Q_{h 0}$	$f_{t}$		$f_{c}$		`HP`
`AH`	`BH`	`CH`		`DH`
`AS`	`BS`	`DF`			`DFLAG`	`DTYPE`	`IREG`
`WF`	`WF1`	`FT1`		`EFC`

定義


フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	（オプション）単位の識別子。（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`	ヤング率（実数）	$[Pa]$
$ν$	ポアソン比。（実数）
`IDEL`	要素削除フラグ。 =1（デフォルト）非アクティブ。 = 2 アクティブ（整数）
`IRATE`	速度依存フラグ。 =1（デフォルト）非アクティブ。 = 2 アクティブ（整数）
`FCUT`	ひずみ速度フィルタリング周波数。デフォルト= 10 kHz（実数）	$[Hz]$
`ECC`	偏心量。デフォルト：コメント6（実数）
$Q_{h 0}$	初期硬化。デフォルト = 0.3（実数）
$f_{t}$	引張時の強度限界。（実数）	$[Pa]$
$f_{c}$	圧縮時の強度限界。（実数）	$[Pa]$
`HP`	硬化係数。（実数）
`AH`	圧縮損傷第1 延性パラメータ。デフォルト = 0.08（実数）
`BH`	圧縮損傷第2 延性パラメータ。デフォルト = 0.003（実数）
`CH`	圧縮損傷第3 延性パラメータ。デフォルト = 2.0（実数）
`DH`	圧縮損傷第4 延性パラメータ。デフォルト = 1.0E-6（実数）
`AS`	第1延性測定パラメータ4 デフォルト = 15.0（実数）
`BS`	第2延性測定パラメータ。デフォルト = 1.0（実数）
`DF`	膨張係数。デフォルト = 0.85（実数）
`DFLAG`	損傷モデルタイプ。 =1（デフォルト）非対称損傷 = 2 等方性 = 3 乗算（整数）
`DTYPE`	引張損傷形状。 = 1 線形 =2（デフォルト）双線形 = 3 指数（整数）
`IREG`	正規化フラグ。 = 1 非アクティブ =2（デフォルト）アクティブ（整数）
`WF`	破壊時の引張非弾性変位/ひずみ。次元は`IREG`パラメータ値に依存します。 4 7 （実数）	$[m]$
`WF1`	軟化曲線変化における引張弾性変位/ひずみ（双線形損傷のみ）。次元は`IREG`パラメータ値に依存します。 4 デフォルト = 0.15*`WF` （実数）	$[m]$
`FT1`	`WF1`での引張強さ。デフォルト = 0.3*`FT` （実数）	$[Pa]$
`EFC`	破壊に近い圧縮非弾性ひずみ。 8 デフォルト = 1.0E-4（実数）

例

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW124/1/1
Concrete CDPM2
#        Init. dens.
              2.3E-9                  
#                  E                  NU                IDEL               IRATE                FCUT
               28000                0.19                   1                   2                   0
#                ECC                 QH0                  FT                  FC                  HP
                   0                   0                 3.5                33.6                 0.5
#                 AH                  BH                  CH                  DH
                   0                   0                   0                   0
#                 AS                  BS                  DF               DFLAG     DTYPE      Ireg
                   0                   0                   0                   1         1         1
#                 WF                 WF1                 FT1                 EFC     
               0.006                   0                   0              0.0005  
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

CDPM2材料則は、いくつかの現象を考慮した使いやすいコンクリート材料則です。この構成モデルは少ないパラメータで設定が可能です。必要な物理パラメータは以下の通りです：

$E$

ヤング率

$ν$

ポアソン比

$f_{t}$

引張強度

$f_{c}$

圧縮強度

$G_{f}^{t}$

引張破壊エネルギー

$G_{f}^{c}$

（オプション）圧縮破壊エネルギー
この法則では、弾性挙動は等方的であると仮定されています。塑性挙動は、次の降伏関数(図 1)で計算されます：
$f_{p} = {\{[1 - q_{h 1} (κ_{p})] {(\frac{\bar{ρ}}{\sqrt{6} f_{c}} + \frac{{\bar{σ}}_{v}}{f_{c}})}^{2} + \sqrt{\frac{3}{2}} \frac{\bar{ρ}}{f_{c}}\}}^{2} + m_{0} q_{h 1}^{2} (κ_{p}) q_{h 2} (κ_{p}) [\frac{\bar{ρ}}{\sqrt{6} f_{c}} r (\cos \bar{θ}) + \frac{{\bar{σ}}_{v}}{f_{c}}] - q_{h 1}^{2} (κ_{p}) q_{h 2}^{2} (κ_{p})$
ここでは、応力空間におけるHaigh-Westergaard座標が考慮されています：
${\bar{σ}}_{v} = \frac{tr (σ)}{3}$ 、 $\bar{ρ} = \sqrt{2 J_{2}} = \sqrt{s : s}$ 、 $\bar{θ} = \frac{1}{3} \arccos (\frac{3 \sqrt{3}}{2} \frac{J_{3}}{J_{2}^{3 / 2}})$
ここで、

$κ_{p}$

硬化変数

$f_{c}$

圧縮での限界強度

$f_{t}$

引張での限界強度

$m_{0}$

偏心の影響を考慮したパラメータ $e_{c c}$

$m_{0} = \frac{3 (f_{c}^{2} - f_{t}^{2})}{f_{c} f_{t}} \frac{e_{c c}}{e_{c c} + 1}$
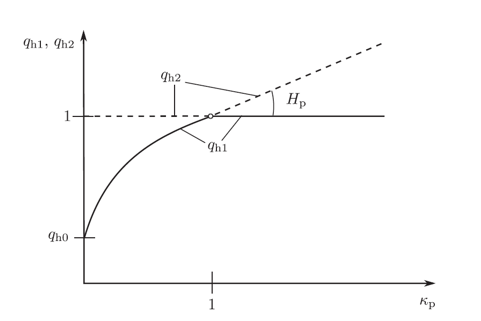
図 1. CDPM2モデルの降伏関数形状（Grasslより）

$q_{h 1}$ と $q_{h 2}$ は、(図 2)で定義される2つの硬化関数です。
$q_{h 1} (κ_{p}) = \{\begin{matrix} q_{h 0} + (1 - q_{h 0}) (κ_{p}^{3} - 3 κ_{p}^{2} + 2 κ_{p}) & i f & κ_{p} < 1 \\ 1 & i f & κ_{p} \geq 1 \end{matrix}$
$q_{h 2} (κ_{p}) = \{\begin{matrix} 1 & i f & κ_{p} < 1 \\ 1 + H_{p} (κ_{p} - 1) & i f & κ_{p} \geq 1 \end{matrix}$
図 2. 硬化関数形状（Grasslより）

ここで、 $q_{h 0}$ は、 $0 < q_{h 0} < 1$ となるように定義された初期硬化です。 $H_{p}$ は硬化係数で、推奨値は0.5です。内部変数 $κ_{p}$ の変遷は以下の通り。
引張と圧縮の間の偏差断面形状を特定するのにWilliam-Warnke関数が使用されます(図 1)。
$r (\cos \bar{θ}) = \frac{4 (1 - e_{c c}^{2}) \cos^{2} \bar{θ} + {(2 e_{c c} - 1)}^{2}}{2 (1 - e_{c c}^{2}) \cos \bar{θ} + (2 e_{c c} - 1) \sqrt{4 (1 - e_{c c}^{2}) \cos^{2} \bar{θ} + 5 e_{c c}^{2} - 4 e_{c c}}}$
塑性ひずみの変遷は、以下の式を用いた非関連塑性ポテンシャルによって定義されます：
$g_{p} = {\{[1 - q_{h 1} (κ_{p})] {(\frac{\bar{ρ}}{\sqrt{6} f_{c}} + \frac{{\bar{σ}}_{v}}{f_{c}})}^{2} + \sqrt{\frac{3}{2}} \frac{\bar{ρ}}{f_{c}}\}}^{2} + q_{h 1}^{2} (κ_{p}) [\frac{m_{0} \bar{ρ}}{\sqrt{6} f_{c}} + \frac{m_{g}}{f_{c}}]$
ここで、
$m_{g} = A_{g} B_{g} f_{c} \exp \frac{{\bar{σ}}_{v} - q_{h 2} \frac{f_{t}}{3}}{B_{g} f_{c}}$
$A_{g} = \frac{3 f_{t} q_{h 2}}{f_{c}} + \frac{m_{0}}{2}$
$B_{g} = \frac{(\frac{q_{h 2}}{3}) (1 + \frac{f_{t}}{f_{c}})}{\ln A_{g} - \ln (2 D_{f} - 1) - \ln (3 q_{h 2} + \frac{m_{0}}{2}) + \ln (D_{f} + 1)}$
ここで、 $D_{f}$ は膨張パラメータ。
この塑性ポテンシャルは、塑性ひずみテンソルの進展を計算するために使用されます。したがって内部変数 $κ_{p}$ の進展は以下のようになります：
${\dot{κ}}_{p} = \frac{‖{\dot{ε}}_{p}‖}{x_{h} ({\bar{σ}}_{v})} (2 \cos^{2} \bar{θ})$
ここで、 $x_{h} = \{\begin{matrix} A_{h} - (A_{h} - B_{h}) \exp (\frac{- R_{h} ({\bar{σ}}_{v})}{C_{h}}) & if & R_{h} ({\bar{σ}}_{v}) \geq 0 \\ E_{h} \exp (\frac{R_{h} ({\bar{σ}}_{v})}{F_{h}}) + D_{h} & if & R_{h} ({\bar{σ}}_{v}) < 0 \end{matrix}$
ここで、 $‖{\dot{ε}}_{p}‖$ は塑性ひずみテンソルの増分のユークリッドノルムです。
CDPM2モデルは、引張と圧縮の間で非対称な損傷進展を考慮します。これらの変数はそれぞれ $ω_{t}$ と $ω_{c}$ で示されます。損傷変数の変遷は、次のように定義されたひずみ基準によって引き起こされます：
$ε_{e q} = \frac{ε_{0} m_{0}}{2} (\frac{\bar{ρ}}{\sqrt{6} f_{c}} r (\cos \bar{θ}) + \frac{{\bar{σ}}_{v}}{f_{c}}) + \sqrt{\frac{ε_{0}^{2} m_{0}^{2}}{4} {(\frac{\bar{ρ}}{\sqrt{6} f_{c}} r (\cos \bar{θ}) + \frac{{\bar{σ}}_{v}}{f_{c}})}^{2} + \frac{3 ε_{0}^{2} {\bar{ρ}}^{2}}{2 f_{c}^{2}}} \geq ε_{0} = \frac{f_{t}}{E}$
この基準に達すると、対応する荷重ケース（引張または圧縮）の損傷履歴変数が更新されます：
- 引張りの場合：
  $κ_{d t 2}^{n} = κ_{d t 2}^{n - 1} + \frac{\max (ε_{e q} - κ_{d t}^{n - 1}, 0)}{x_{s}}$ 、 $κ_{d t 1}^{n} = κ_{d t 1}^{n - 1} + \frac{Δ ε_{p}}{x_{s}}$ 、および $κ_{d t}^{n} = ε_{e q}^{n}$
- 圧縮の場合：
  $κ_{d c 2}^{n} = κ_{d c 2}^{n - 1} + \frac{α_{c} \max (ε_{e q} - κ_{d c}^{n - 1}, 0)}{x_{s}}$ 、 $κ_{d c 1}^{n} = κ_{d c 1}^{n - 1} + α_{c} β_{c} \frac{Δ ε_{p}}{x_{s}}$ および $κ_{d c}^{n} = α_{c} ε_{e q}^{n}$
  ここで、
  $α_{c} = \sum_{i} \frac{{〈σ_{p i}〉}_{-} ({〈σ_{p i}〉}_{+} + {〈σ_{p i}〉}_{-})}{{‖σ_{p}‖}^{2}}$ 、 $β_{c} = \frac{f_{t} q_{h 2} (κ_{p}) \sqrt{2 / 3}}{\bar{ρ} \sqrt{1 + 2 D_{f}^{2}}}$ 、 $x_{s} = 1 + (A_{s} - 1) R_{s}^{B S}$ と $R_{s} = \{\begin{matrix} - \frac{\sqrt{6} {\bar{σ}}_{v}}{\bar{ρ}} & if & {\bar{σ}}_{v} \leq 0 \\ 0 & if & {\bar{σ}}_{v} > 0 \end{matrix}$
非弾性ひずみは、損傷履歴変数から以下の式で求めることができます：
$ε_{i n e l}^{t} = κ_{d t 1} + ω_{t} κ_{d t 2}$ および $ε_{i n e l}^{c} = κ_{d c 1} + ω_{c} κ_{d c 2}$
損傷履歴変数は、最終的に対応する損傷変数の更新を可能にします。
引張損傷に関しては、DTYPEパラメータ値に応じて、3つの異なる進展形状が利用可能です：
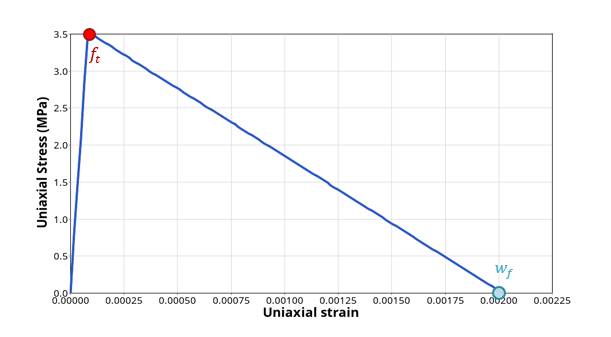
- DTYPE = 1: 線形損傷 $f_{t}$ は損傷開始時の強度限界、 $w_{f}$ は剛性がヌルになる破壊変位 (図 3)。
  $ω_{t} = \frac{E κ_{d t} w_{f} - f_{t} w_{f} + f_{t} κ_{d t 1} h}{E κ_{d t} w_{f} - f_{t} h κ_{d t 2}}$
  図 3. 線形損傷進展を用いた単一ユニット要素の単軸引張試験. $f_{t}$ =3.5MPa、 $w_{f}$ =0.002mm。
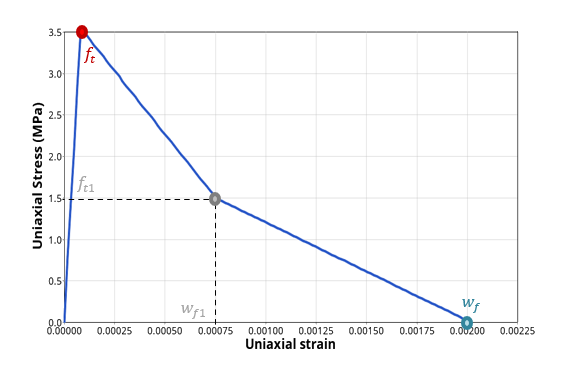
- DTYPE = 2: 双線形損傷は、線形損傷と似ていますが、損傷の増分が傾きを変えるポイントを定義する $w_{f 1}$ と $f_{t 1}$ の2つの値を使用する点が異なります(図 4)。
  $ω_{t} = \{\begin{matrix} \frac{E κ_{d t} w_{f 1} - f_{t} w_{f 1} - (f_{t 1} - f_{t}) κ_{d t 1} h}{E κ_{d t} w_{f 1} + (f_{t 1} - f_{t}) h κ_{d t 2}} & if & \begin{matrix} h ε_{i n e l}^{t} > 0 & and & h ε_{i n e l}^{t} < w_{f 1} \end{matrix} \\ \frac{E κ_{d t} (w_{f} - w_{f 1}) - f_{t 1} (w_{f} - w_{f 1}) + f_{t 1} κ_{d t 1} h - f_{t 1} w_{f 1}}{E κ_{d t} (w_{f} - w_{f 1}) - f_{t 1} h κ_{d t 2}} & if & \begin{matrix} h ε_{i n e l}^{t} > w_{f 1} & and & h ε_{i n e l}^{t} < w_{f} \end{matrix} \end{matrix}$
  図 4. 双線形損傷進展を用いた単一ユニット要素の単軸引張試験. $f_{t 1}$ =3.5MPa、 $f_{t}$ =1.5MPa、 $w_{f 1}$ =0.00075mm、 $w_{f}$ =0.002mm。
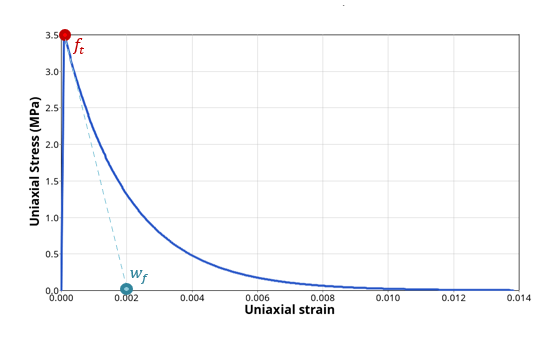
- DTYPE = 3: 変位しきい値 $w_{f}$ が、単軸のひずみ軸と応力軟化の始まりの接線の交点に対応する指数損傷 (図 5)。
  $ω_{t} = 1 - \exp (- \frac{h ε_{i n e l}^{t}}{w_{f}})$
  図 5. 指数損傷進展を用いた単一ユニット要素の一軸引張試験. $f_{t}$ =3.5 MPa、 $w_{f}$ =0.002 mm。
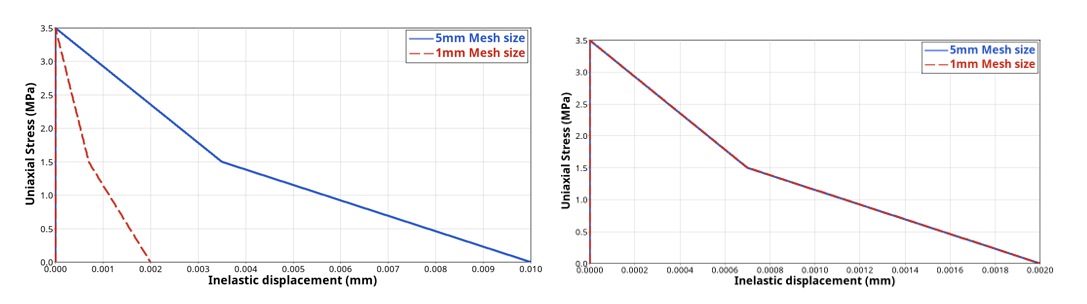
これらの異なる式において、 $h$ はメッシュサイズ依存を避けるために使用できるパラメータです。IREG = 1の場合、正規化手法は使用されず、 $h$ が1に設定されます。その場合、限界値 $w_{f}$ は無次元の限界ひずみとなります。それ以外の場合は、IREG = 2の場合、Hillerborgの正規化手法 ^² (Crack Brand法 ^³)が使用され、 $h$ は初期要素サイズに等しくなります。すると、限界値 $w_{f}$ は変位と同質の限界変位になります。Hillerborgの正規化手法は、 $G_{f}^{t}$ で示される引張破壊エネルギーが、どのような要素サイズを用いても一定に保たれるようにするものです(図 6)。
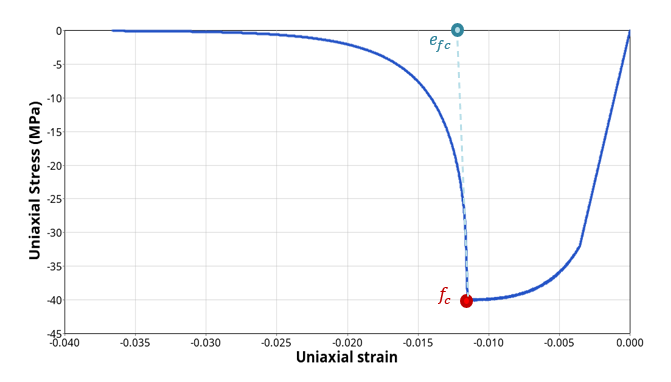
図 6. IREQ = 0（左）、IREQ = 1（右）の2つの異なるメッシュサイズにおける双線形損傷による単軸引張試験。

圧縮損傷に関しては、正規化手法を用いない指数関数的な進展形状のみ有効です(図 7)。メッシュサイズ依存性はそれほど敏感ではないと想定されます。
$ω_{c} = 1 - \exp (- \frac{ε_{i n e l}^{c}}{e_{f c}})$
図 7. 単一ユニット要素の単軸圧縮試験. ここで、 $e_{f c} = 5 × 10^{(- 4)}$
応力計算における損傷の影響は、DFLAGパラメータ値によって異なります：
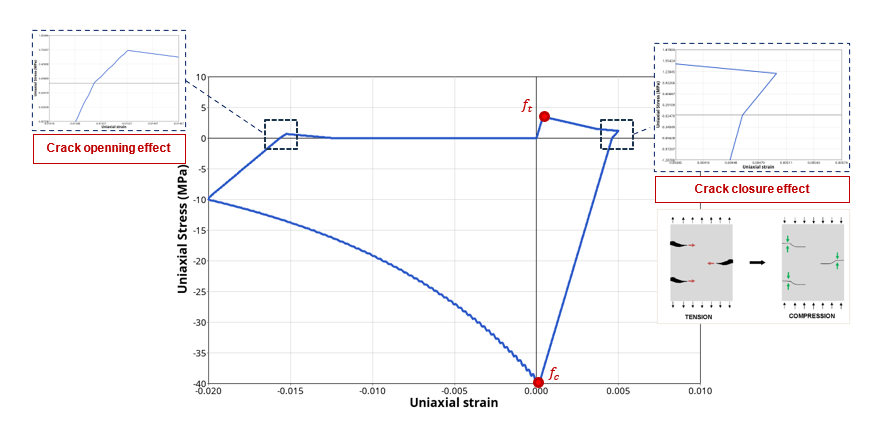
- DFLAG = 1: 引張から圧縮に切り替わる際の亀裂閉口を考慮し、初期剛性を回復させる非対称軟化。反対に、引張から圧縮に切り替えると、すでにある亀裂が再び開きます。（図 8）。
  $σ = (1 - ω_{t}) σ_{e f f}^{t} + (1 - ω_{c}) σ_{e f f}^{c}$
  ここで、 $σ_{e f f}^{t}$ と $σ_{e f f}^{c}$ はそれぞれ、損傷していない（有効な）応力テンソルの引張部分と圧縮部分です。
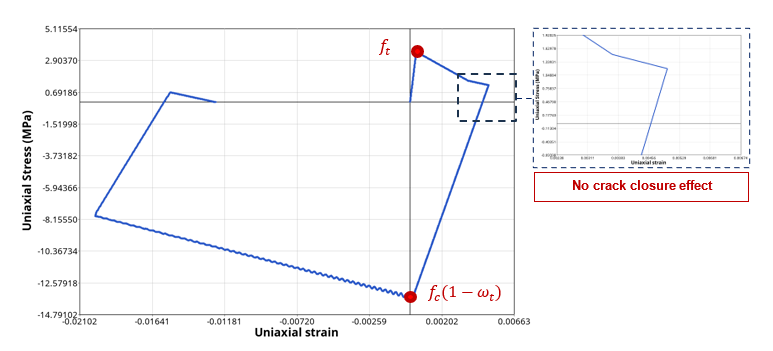
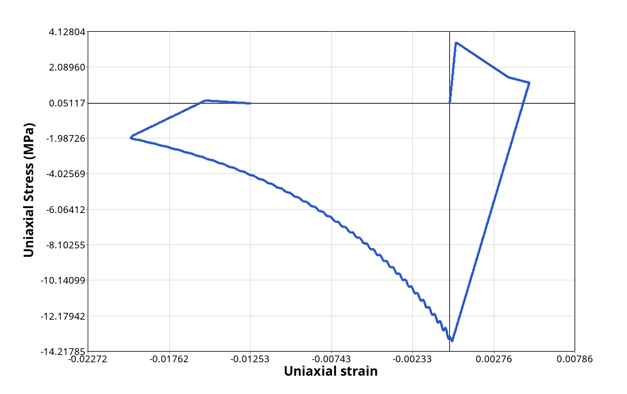
  図 8. 非対称損傷軟化を伴う載荷 / 除荷単軸試験
- DFLAG = 2: 引張と圧縮の両方における引張損傷の影響のみを考慮した等方軟化。この場合、亀裂閉口は考慮されません。引張から圧縮、またはその反対に切り替えても、剛性の変化は見られません(図 9)。また、引張損傷は圧縮での進展は少ないと考えられます。
  $σ = (1 - ω_{t}) σ_{e f f}$
  図 9. 等方性損傷軟化を伴う載荷 / 除荷単軸試験
- DFLAG = 3: 引張と圧縮の両損傷の影響が考慮され、累積される乗法的軟化(図 10)。
  $σ = (1 - (1 - ω_{t}) (1 - ω_{c})) σ_{e f f}$
  図 10. 乗法的損傷軟化を伴う載荷 / 除荷単軸試験
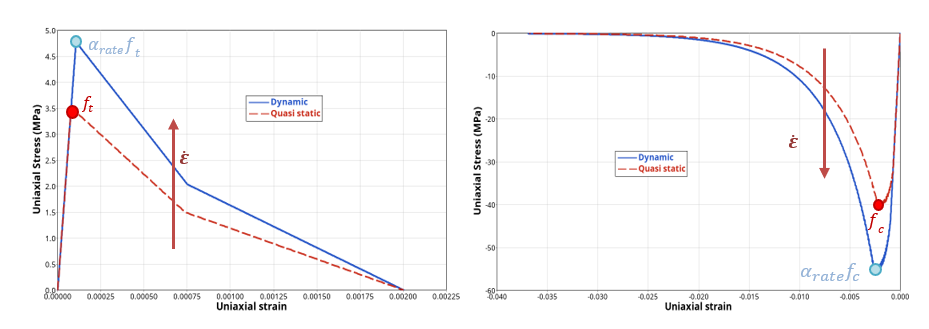
CDPM2モデルで考慮される最後の現象はひずみ速度依存性です。ひずみ速度が大きい場合、コンクリートは引張または圧縮強度の限界が大きくなる可能性が高くなります。これは以下の式を導入します：
$f_{t}^{r a t e} = α_{r a t e} f_{t}$ 、 $f_{c}^{r a t e} = α_{r a t e} f_{c}$ および $f_{t 1}^{r a t e} = α_{r a t e} f_{t 1}$
DIF（Dynamic Increase Factor） $α_{r a t e}$ は以下で計算されます：
$α_{r a t e} = (1 - α_{c}) α_{r a t e}^{t} + α_{c} α_{r a t e}^{c}$
ここで、 $α_{c}$ は、コメント3の損傷履歴変数の式で定義された圧縮係数です。
コンクリートは圧縮よりも引張の方がひずみ速度の影響を受けやすいため、引張と圧縮ではひずみ速度依存性が異なります。引張と圧縮の2つの動的増加係数は次のように計算されます：
$α_{r a t e}^{t} = \{\begin{matrix} 1 & for & {\dot{ε}}_{\max} \leq 30 \times 10^{- 6} s^{- 1} \\ {(\frac{\dot{ε}}{{\dot{ε}}_{t 0}})}^{δ_{s}} & for & 30 \times 10^{- 6} s^{- 1} < {\dot{ε}}_{\max} \leq 1 s^{- 1} \\ β_{s} {(\frac{\dot{ε}}{{\dot{ε}}_{t 0}})}^{\frac{1}{3}} & for & 1 s^{- 1} \leq {\dot{ε}}_{\max} \end{matrix}$ ここで、 $δ_{s} = \frac{1}{1 + 8 \frac{f_{c}}{f_{c 0}}}$ 。 $\log β_{s} = 6 δ_{s} - 2$
$α_{r a t e}^{c} = \{\begin{matrix} 1 & for & {\dot{ε}}_{\max} \leq 30 \times 10^{- 6} s^{- 1} \\ {(\frac{\dot{ε}}{{\dot{ε}}_{c 0}})}^{1.026 α_{s}} & for & 30 \times 10^{- 6} s^{- 1} < {\dot{ε}}_{\max} \leq 30 s^{- 1} \\ γ_{s} {(\frac{\dot{ε}}{{\dot{ε}}_{c 0}})}^{\frac{1}{3}} & for & {30s}^{- 1} \leq {\dot{ε}}_{\max} \end{matrix}$ ここで、 $α_{s} = \frac{1}{5 + 9 \frac{f_{c}}{f_{c 0}}}$ 。 $\log γ_{s} = 6.56 α_{s} - 2$
等価ひずみ速度の偏差 $\dot{ε}$ は、上記の式でDIFを計算するために使用されます。
ひずみ速度の影響については、パラメータを特定する必要はありません。フラグIRATEを2に設定するだけです。図 11 は、CDPM2の挙動に対するひずみ速度の影響が予想される傾向を示しています。実験でよく見られるように、引張/圧縮の強度限界を上げることで、破壊時の散逸エネルギーも影響を受けます。
図 11. ひずみ速度依存性を有する引張/圧縮単軸試験 (IRATE = 1)
偏心値のデフォルト値は次のようにして得られます：
$ε_{i} = \frac{f_{t} ({(1.16 f_{c})}^{2} - f_{c}^{2})}{1.16 f_{c} (f_{c}^{2} - f_{t}^{2})}$ および $e_{c c} = \frac{1 + ε_{i}}{2 - ε_{i}}$
引張破壊エネルギー、 $G_{f}^{t}$ はモデルの入力として直接使用されませんが、破壊時の引張非弾性変位/ひずみの値を計算するために使用されます。 $w_{f}$ 。
線形軟化則（DTYPE = 1）の場合、引張破壊エネルギーは次のようになります：
$w_{f} = \frac{2 G_{f}^{t}}{f_{t}}$ （IREG = 2の場合、デフォルト）
$w_{f} = \frac{2 G_{f}^{t}}{h f_{t}}$ （IREG = 1の場合、h = 識別のための基準要素サイズ）
双線形軟化則（DTYPE = 2）の場合、引張破壊エネルギーは次のようになります：
$G_{f}^{t} = \frac{f_{t} w_{f 1}}{2} + \frac{σ_{1} w_{f}}{2}$
仮に $σ_{1} / f_{t}$ = 0.3であり $w_{f 1} / w_{f}$ = 0.15の場合以下のようになります：
$w_{f} = \frac{G_{f}^{t}}{0.225 f_{t}}$ （IREG = 2の場合、デフォルト）
$w_{f} = \frac{G_{f}^{t}}{0.225 f_{t} h}$ （IREG = 1の場合、h = 識別のための基準要素サイズ
圧縮破壊エネルギー、 $G_{f}^{c}$ はモデルの入力として直接使用されませんが、破壊に近い圧縮非弾性ひずみの値を計算するために使用されます：
$ε_{f}^{c} = \frac{G_{f}^{c}}{f_{c} h A_{s}}$
このとき、h = 識別のための基準要素サイズ、および $A_{s}$ は延性の尺度です：
$x_{s} = 1 + (A_{s} - 1) R_{s}^{B S}$
全体損傷変数は、/ANIM/BRICK/DAMGまたは/HED/SOLID/DAMGを使用して出力されます。

¹ Peter Grassl, Dimitrios Xenos, Ulrika Nyström, Rasmus Rempling, Kent Gylltoft, CDPM2: A damage-plasticity approach to modelling the failure of concrete, International Journal of Solids and Structures, Volume 50, Issue 24, 2013, Pages 3805-3816, ISSN 0020-7683

² A. Hillerborg, M. Modéer, P.-E. Petersson, Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements, Cement and Concrete Research, Volume 6, Issue 6, 1976, Pages 773-781, ISSN 0008-8846

³ Bažant, Z.P., Oh, B.H. Crack band theory for fracture of concrete. Mat. Constr. 16, 155–177 (1983)

/MAT/LAW124 (CDPM2)

フォーマット

定義

例

コメント