MV-3022：4節リンクモデルの最適化

本チュートリアルでは、4つのリンクから成るモデルについてMotionViewのOptimization Wizardを使って最適化問題をセットアップします。

以下について習得します：
  • 設計変数としてのポイントの座標の定義
  • カーブにマッチングさせるための応答タイプ'Root Mean Square Deviation'を定義
  • 目的関数としての応答の使用
  • 最適化の実行と結果のポスト処理
  • （オプション） MotionSolve最適化における実行不可能な設計
概要
本チュートリアルでは、4つのリンクから成る機構のジョイントの位置を最適化し、カプラーの希望する運動を取得します。感度の計算には、MotionSolveのDSA（Design Sensitivity Analysis： 設計感度解析）機能が使用されます。
図 1. ジョイントタイプなしの4節リンクモデル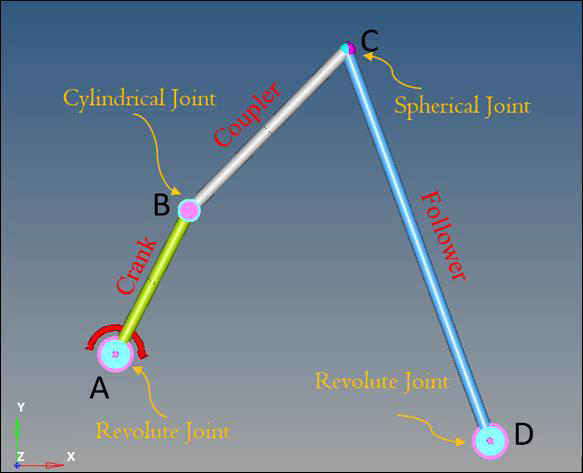


モデル全体は、これら4つの設計ポイントA、B、C、Dの形でパラメータ化されます。モデルは2D空間（X-Y面）で作動するため、結果的に設計変数は8つになります。初期の設計は表 1のようにリストされます：
表 1.
Point X Y
A -45 45
B 65 260
C 300 500
D 515 -85

モデルの確認

このステップでは、MotionViewで、4つのリンクから成るモデルを解析します。

開始に先立ち、mbd_modeling\motionsolve\optimization\MV-3022にあるmv_3022_initial_4bar_opt.mdlファイルを自身の<作業ディレクトリ>にコピーします。
  1. ファイルmv_3022_initial_4bar_opt.mdlをMotionViewで開きます。
  2. モデルのエンティティを確認します。
    1. XおよびY方向のモーションを定義するカーブDesired Coupler Path DXおよびDesired Coupler Path DYが設定されていることを確認します。
    2. カーブを使って希望する運動を計測する出力Desired Coupler Trajectoryが設定されていることを確認します。
    3. カプラーボディの重心変位を計測する出力Actual Coupler Trajectoryが設定されていることを確認します。
      図 2.


設計変数の追加

  1. Project BrowserでModelを右クリックし、context menuからOptimization Wizardを選択します。
  2. Design Variablesページで、Pointsタブをクリックします。
    ポイントが図 3にリストされます：
    図 3. Optimizationウィザード – Pointsタブ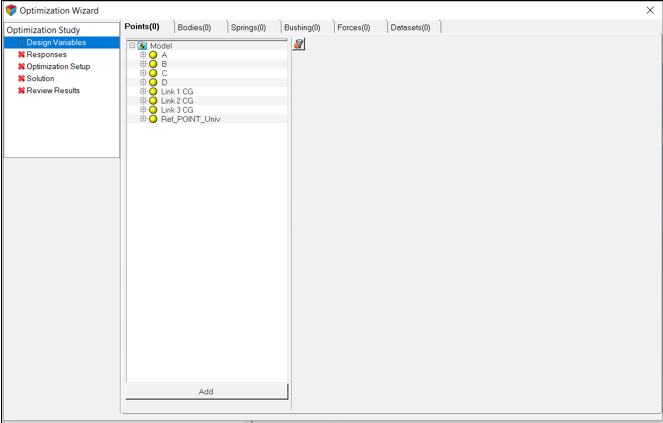


  3. ポイントA、B、C、Dについて、xおよびy座標を設計変数とします。（Filter datamembers）アイコンをクリックします。
  4. FilterダイアログでZチェックボックスをクリックしてオフにします。
    図 4.
  5. OKをクリックします。
  6. Model Treeで、Point A、Point B、Point C、およびPoint Dを選択します。続いて、Addをクリックします。
  7. 設計変数の上限および下限を、表 2に従って修正します：
    表 2.
    DV 下限値 上限値
    Point A(DV) - X -50 50
    Point A(DV) - Y -50 50
    Point B(DV) - X 20 80
    Point B(DV) - Y 180 280
    Point C(DV) - X 240 380
    Point C(DV) - Y 400 620
    Point D(DV) - X 180 520
    Point D(DV) - Y -100 20
    これで、設計変数の設定が終わりました。

応答変数の追加

ここで、最適化のための応答変数を追加します。

この最適化の目的は、カプラーをパスに沿って動かすことにあります。これを達成するために、以下の2つの応答を作成します：
  • カプラー重心の軌道 – DX
  • カプラー重心の軌道 – DY
上記のカプラーモーションのカーブは、Root Mean Square Deviation（RMS2）タイプの応答変数を使って、それぞれのターゲットカーブとマッチングさせる必要があります。この応答の詳細は、 Multibody Optimization User’s GuideおよびMotionViewユーザーズガイドから得ることができます。
  1. Responsesページ上をクリックします。
  2. ボタンをクリックします。
  3. Labelを'rms2_dx'に変更します。
  4. OKをクリックして、応答変数を追加します。
  5. 応答変数が作成されたら、Response Typeの下でRoot Mean Square Deviationを選択します。
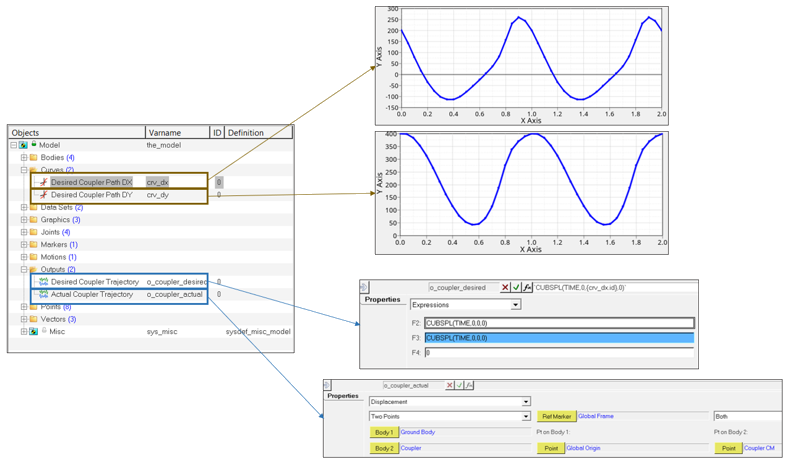
  6. Curveコレクターをダブルクリックし、Desired Curveのユーザー入力にDesired Coupler Path DXを選択します。これは、カプラーDXのターゲットカーブです。
  7. Response Expressionに式`DX({b_bc.cm.id})`（カプラーボディの重心のDX）と入力します。
  8. 手順に再度従い、もう1つのRoot Mean Square Deviation応答を作成します。詳細には表 3を使用します。
    表 3.
    RV Desired Curve Response Expression
    rms2_dx Desired Coupler Path DX `DX({b_bc.cm.id})`
    rms2_dy Desired Coupler Path DY `DY({b_bc.cm.id})`
    Responsesページは、図 5に示すように見えるはずです：
    図 5. 完了した応答のページ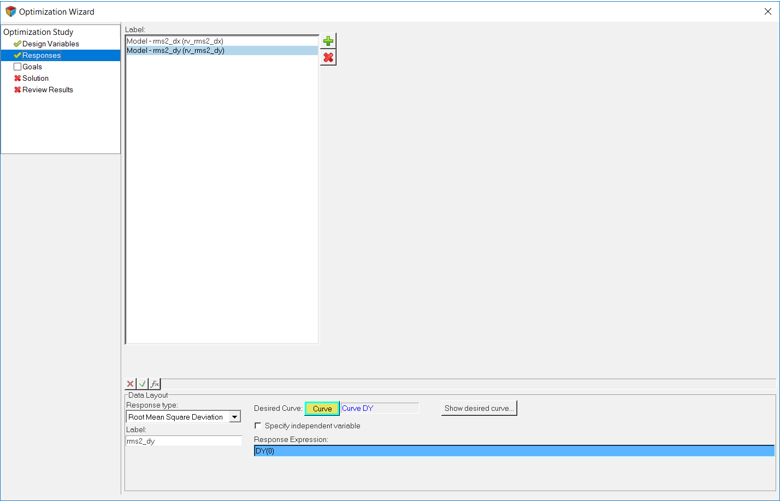


目的関数と制約条件の追加

このステップでは、2つの目的関数を問題に追加します。

この問題の目的は、カプラーDXとDYのモーションが、最適化の最後におけるターゲットのカーブと一致することです。この前のセクションで作成した応答を目的関数として使うことができます。

  1. Goalsページに進みます。
  2. Objectivesの下で、をクリックします。
    これで、応答rv_rms2_dxで目的関数が追加されます。
  3. Weightに1.0を選択し、Typeはmin（応答を最小にしたい）のままとします。
  4. これらの手順を繰り返し、もう一つの目的関数を追加します。2つ目の目的関数にはrv_rms2_dyを選択します。
  5. Weightに1.0を選択し、Typeはminのままとします。
    この問題では、制約条件はありません。したがって、モデルのセットアップは完了です。これで、モデル実行の準備が整いました。
    図 6. 目的関数の定義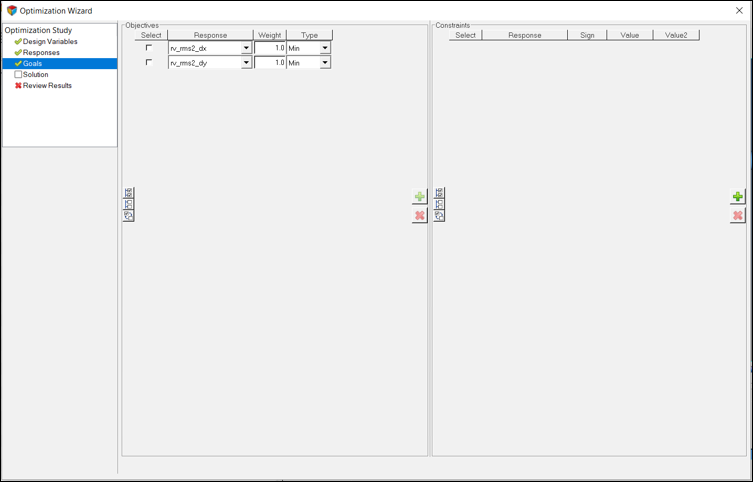


最適化の実行

ここで、最適化を実行します。

  1. Solutionsページに進みます。
  2. Plot Optimization Summary のチェックボックスを有効にします。
  3. Save & Optimizeをクリックして最適化を開始します。
    最適化プロセスが完了すると、テキストウィンドウには最適化された設計変数値、応答の最終値および最適化されたコスト関数が表示されます。
    図 7. 最適化完了後のOptimizationテキストウィンドウ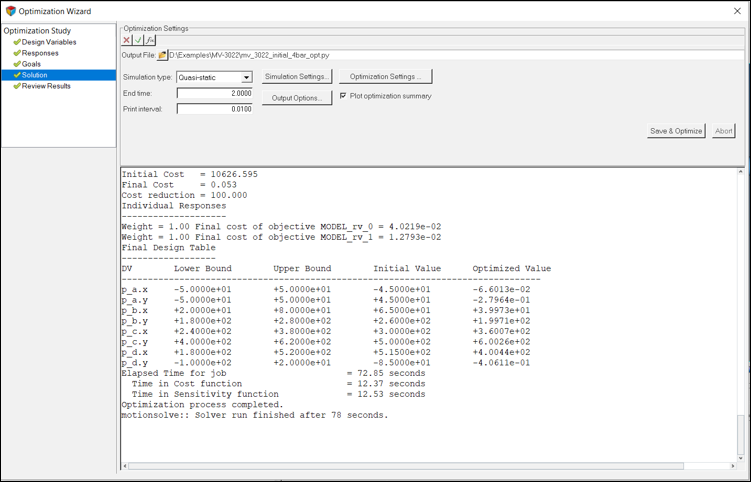


    期待される設計変数の値は表 4に示すとおりです：
    表 4.
    DV 期待される値 最適化エンジンからの値
    p_0.x 0 -0.0660
    p_0.y 0 -0.2796
    p_1.x 40 39.97
    p_1.y 200 199.71
    p_2.x 360 360.07
    p_2.y 600 600.26
    p_3.x 400 400.44
    p_3.y 0 -0.0406

ポスト処理

このステップでは、最適化の結果をポスト処理します。

  1. 解析が完了したら、Review Resultsページに進みます。
    Summaryタブは、設計変数、応答および目的関数の履歴を表形式でリストします。このチュートリアルでは、最適設計変数は、反復計算27からのものとなっています。
    図 8. 設計変数、応答、コスト関数を反復計算毎にリストしたSummaryタブ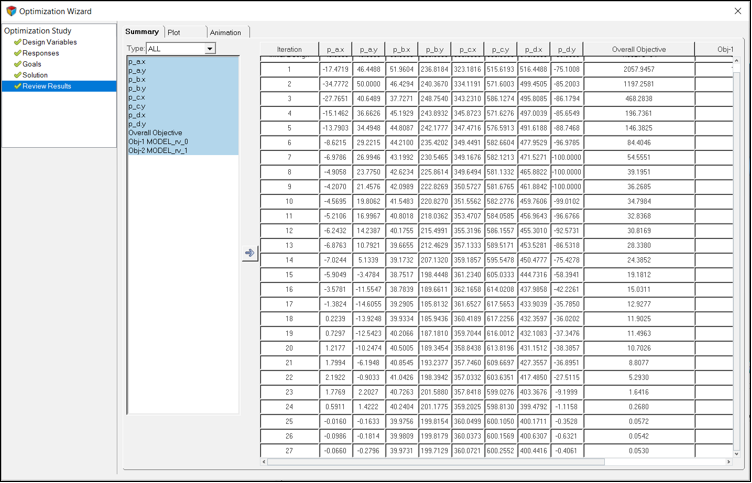


  2. Plotタブをクリックします。Overall ObjectiveとIteration変数をプロットします。
    Plotタブは、設計変数、応答変数およびコスト関数の変動をグラフで可視化する助けとなります。ユーザーは、X軸の変数に対しY軸に任意の変数の数をプロットするよう選ぶことができます。
    図 9. overall objective（logスケール） vs. iteration numberのプロット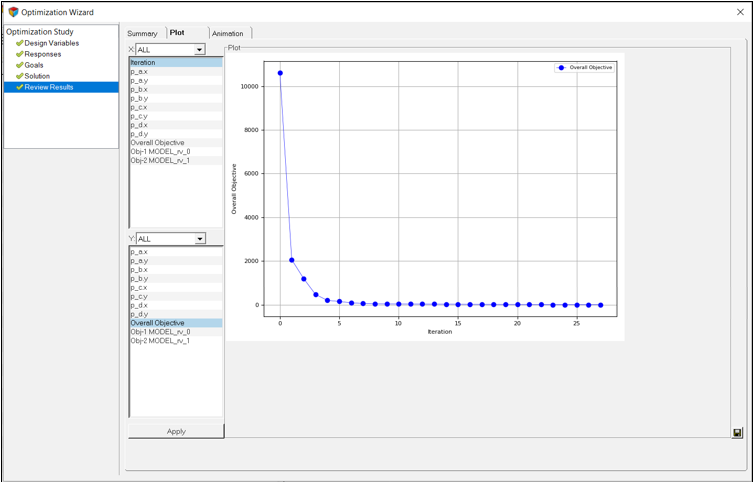


    注: また、反復計算全体を通して特定の設計変数がどのように変化していくかを見ることもできます。例えば、Yリスト内のp_b.x（Point B-X）を選択し、Applyをクリックします。
    図 10.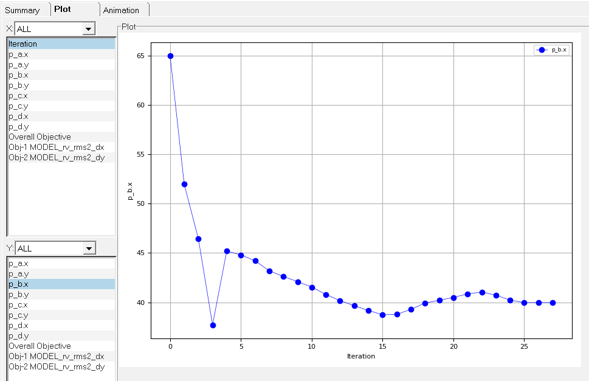


  3. 反復計算中に生成されたコンフィギュレーションをアニメーション表示します。
    1. AnimationタブでIterationドロップダウンメニューから、アニメーション表示したい反復計算の番号を選択します（このチュートリアルではIteration 27を選択します）。
    2. Load Resultをクリックし、選択した反復計算に対応したアニメーションを読み込みます。
    図 11. Post ProcessingページのAnimationタブ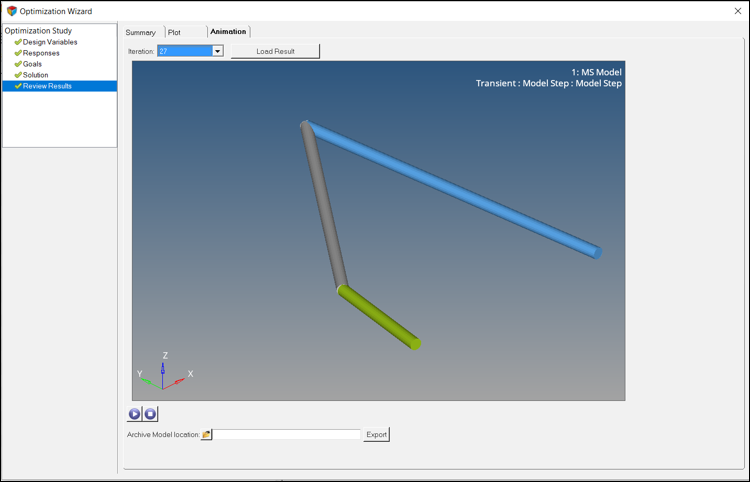


    このタブからは、任意のコンフィギュレーションからモデルのアーカイブをエクスポートするオプションもあります。
  4. Iteration 27から結果を読み込みます。
  5. Archive Model locationブラウザを使用し、ファイルのパスを選択します。
  6. Exportをクリックします。
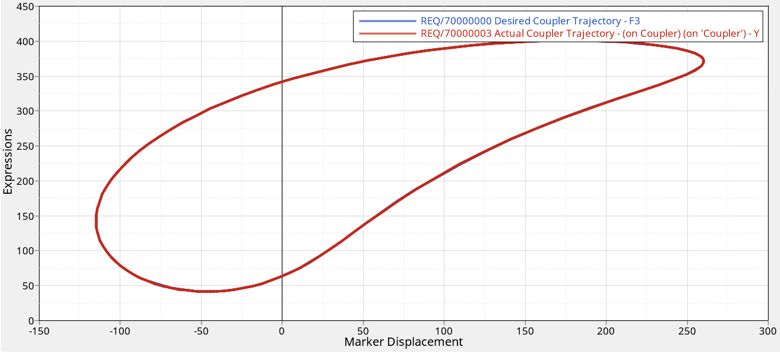
  7. 最適化された結果について、カプラーのパスが希望するターゲットのパスとどのように比較されるかを確認します。
    1. Optimization Wizardを選択します。
    2. MotionViewセッションにページを1つ追加します。
    3. 新しいページでクライアントをHyperGraphに変更します。
    4. 最適化ランの最終反復計算フォルダー内の.abfファイルを開きます。
      注: 最適化ランのディレクトリは解析中に自動的に生成され、py_name_timestampの規則に従って命名されます。ここで、py_nameはSolutionページで与えられているPythonファイルの名称、timestampはソリューションが開始された際の時間です。
      図 12.


    5. XおよびY軸に、以下のType、Request、Componentを選択します：
      表 5.
      Axis Type Request Component
      X Expressions REQ/70000000 Desired Coupler Trajectory F2
      Y Expressions REQ/70000000 Desired Coupler Trajectory F3
      図 13.


    6. Applyをクリックします。
    7. 下記のX軸およびY軸のスペックを使用し、カプラー重心の実際の軌道をプロットします。
      表 6.
      Axis Type Request Component
      X Marker Displacement REQ/70000003 Actual Coupler Trajectory - (on Coupler) (on 'Coupler') X
      Y Marker Displacement REQ/70000003 Actual Coupler Trajectory - (on Coupler) (on 'Coupler') Y
      結果のプロットは互いに重なり合います。
      図 14.


実現不可能 / 可能なリカバリーの特定（オプション）

このステップでは、MotionSolveの強力な機能を使用し、失敗した反復計算からリカバーすることで最適設計を取得します。

機構システムがある種の物理的な制約条件によって制限されることは珍しくありません。この4節リンクの例では、入力リンクをクランクとするために、Grashof制約が満足される必要があります。最適化エンジンが新規設計を選択する際、これらの制約は、最適化の制約条件として追加されるか否かにかかわらず違反することがあります。MotionSolveの最適化エンジンは、そのような実現不可能な設計からリカバーすることを助けるリカバリーモードを有しています。このチュートリアルで最適化エンジンがどのようにリカバーするかを見てみるために、初期設計を変更し、その動作を確認します。

  1. Design Variablesページに戻り、図 15に示すようにNominal、Upper Bound、Lower boundを変更します。
    図 15. 設計変数の値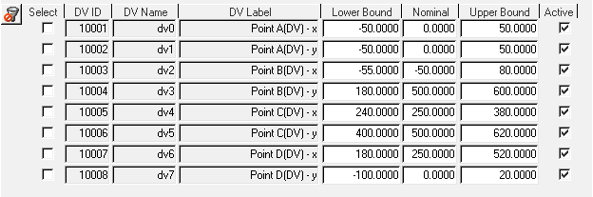


    4つのリンクから成る機構は図 16のように見えるはずです：
    図 16. 設計変数の値を変更した後の4節機構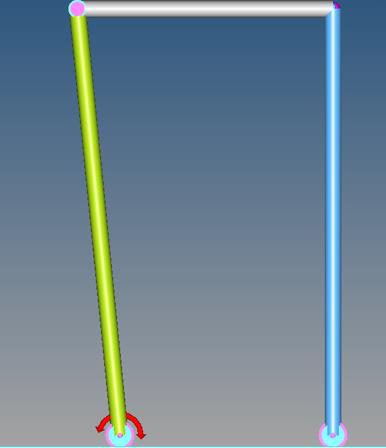


  2. Responses、ObjectivesおよびConstraintsは、本チュートリアルで先に定義したままとします。
  3. Solutionsページで4bar_opt_for_recover.pyとして別の出力ファイルで最適化を実行します。
    反復計算の数は、初期設計の違いで変化します。
    重要: ソルバー出力内の最後の列‘Reduced Step’に着目してください。
    図 17. recoveryモードをオンにした際のソルバー出力


    この例では、最適化エンジンは、反復計算2-7で実現不可能な設計であることを見出し、実現可能な設計になるまでステップサイズを減らすように伝えています。
  4. 出力ファイルを確認します。出力ファイルはほとんどの場合、特定のポイントにおいてソルバーが失敗している原因とそれを回避する方法（可能であれば）をユーザーに示しています。
    図 18. 実現不可能な設計を含むサブフォルダー
    最適化エンジンが実現不可能な設計からリカバーすると、追加のフォルダー‘Infeasible Points’が生成され、各サブフォルダーには下記の情報が含まれるようになります：
    • dvValues.txt：設計変数の値
    • 4bar_opt_for_recover.abf：MotionSolve出力ファイル
    • 4bar_opt_for_recover.h3d：アニメーションファイル（可能な場合のみ出力）
    • 4bar_opt_for_recover.log：MotionSolveログファイル
    • 4bar_opt_for_recover.mrf：MotionSolve出力ファイル
    • 4bar_opt_for_recover.xml：MotionSolve xml入力ファイル
    図 19. 実現不可能な設計のそれぞれについての出力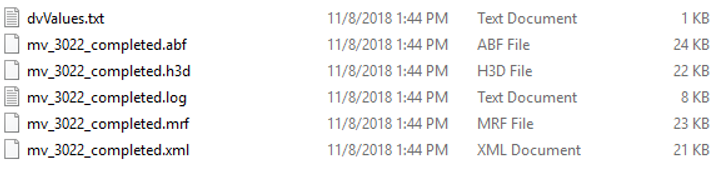


    h3dファイルとログファイルは多くの場合役に立ちます。HyperViewでh3dファイルを読み込み、何が問題であるかを検証します。
  5. フォルダーInfeasible Point 1 -- iter-2内の4bar_opt_for_recover.h3dを読み込みます。
    ソルバーがクラッシュする前にシステムがロックアップポジションに入っていることが見てとれます。
    図 20.


  6. 結果を確認します。

    例に示す結果はSTEP 5で得られたものと非常に似ており、コスト関数は大幅に減じています。これは、中間ステップで実現不可能な設計に遭遇したとしても、最適な設計が得られることを示しています。しかしながら、最適性は保証されない場合もあります。そういった場合、先のステップにおける検証に基づいて適切な制約条件を追加することで、結果を向上させることができます。4つのリンクから成る機構には、Grashof制約を追加できます。MotionSolveでこれを行う方法の例が含まれます。