/MAT/LAW72 (HILL_MMC)

Blockフォーマットキーワード修正Mohr破壊基準を使用して異方性Hill材料を記述します。この材料則は、シェルおよびソリッドに対して使用可能です。

フォーマット


(1)	(3)	(5)	(7)	(9)
/MAT/LAW72/`mat_ID`/`unit_ID`または/MAT/HILL_MMC/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	`v`
$σ_{y}^{0}$	$ε_{p}^{0}$	`n`	`F`	`G`
`H`	`N`	`L`	`M`
`C`₁	`C`₂	`C`₃	`m`	`D`_c

定義


フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	Unit Identifier。（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`	初期ヤング率（実数）	$[Pa]$
`v`	ポアソン比（実数）
$σ_{y}^{0}$	初期降伏応力デフォルト = 10²⁰（実数）	$[Pa]$
$ε_{p}^{0}$	初期塑性ひずみデフォルト = 10^-20（実数）
`n`	Swift硬化の等方性関数の指数部： $σ_{y} = σ_{y}^{0} {(ε_{p} + ε_{p}^{0})}^{n}$ MMC破壊方程式の指数部としても使用します。 2 デフォルト = 1.0（実数）
`F`, `G`, `H`, `L`, `M`, `N`	6つのHILL材料異方性パラメータ（> 0）（実数）
`C`₁	MMC破壊モデルの第1パラメータ（実数）
`C`₂	MMC破壊モデルの第2パラメータデフォルト = $σ_{y}^{0}$ （実数）	$[Pa]$
`C`₃	MMC破壊モデルの第3パラメータ（実数）
`m`	軟化関数の指数部 3 デフォルト = 1.0（実数）
`D`_c	臨界損傷 = 1（デフォルト）損傷が1に達すると要素は削除されます。 > 1 降伏応力は軟化関数によって修正されます 3 損傷が臨界損傷値に達すると、要素は削除されます。（実数）

例（金属）

この材料の例では、材料の軟化と破断を検討します。MMCパラメータC₁、C₂、およびC₃を使用して、単軸引張試験における破断ひずみが0.98と計算されます。m=0.5とした単軸引張試験では0.98で材料の軟化が始まり、0.98 x D_cに達するまで継続します。

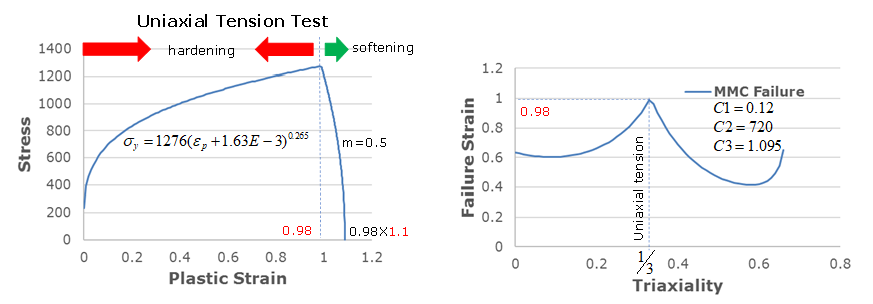
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW72/1/1
Metal
#              RHO_I
              0.0028
#                  E                  nu
              200E+3                 0.3
#               Sig0                Eps0                   n                   F                   G
                1276             1.63E-3               0.265                 0.5                 0.5
#                  H                   N                   L                   M
                 0.5                 1.5                   0                   0
#                 C1                  C2                  C3                   m                  Dc
                0.12                 720               1.095                 0.5                 1.1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

3D等価Hill応力は：
$f = \sqrt{F {(σ_{yy} - σ_{zz})}^{2} + G {(σ_{zz} - σ_{xx})}^{2} + H {(σ_{xx} - σ_{yy})}^{2} + 2 L σ_{yz}^{2} + 2 M σ_{zx}^{2} + 2 N σ_{xy}^{2}}$
シェル要素の場合：
$f = \sqrt{F σ_{yy}^{2} + G σ_{xx}^{2} + H {(σ_{xx} - σ_{yy})}^{2} + 2 N σ_{xy}^{2}}$
MMC破壊基準は：
$D = \int_{0}^{ε_{p}} \frac{d ε_{p}}{ε_{f} (θ, η)}$
ここで、
$ε_{f} (\bar{θ}, η) = {\frac{σ_{y}^{0}}{C_{2}} [C_{3} + \frac{\sqrt{3}}{2 - \sqrt{3}} (1 - C_{3}) (\sec (\frac{\bar{θ} π}{6}) - 1)] [\sqrt{\frac{1 + C_{1}^{2}}{3}} \cos (\frac{\bar{θ} π}{6}) + C_{1} (η + \frac{1}{3} \sin (\frac{\bar{θ} π}{6}))]}^{- \frac{1}{n}}$
- 3次元ソリッド要素の場合
  $η$ は応力の3軸性で、 $η = \frac{\frac{1}{3} (σ_{x x} + σ_{y y} + σ_{z z})}{σ_{V M}}$
  $\bar{θ}$ はシフトLode角 $\bar{θ} = 1 - \frac{2}{π} a r \cos ζ$
  で、Lode角（ $θ$ ）パラメータ $ζ = \cos (3 θ) = \frac{27}{2} \frac{J_{3}}{σ_{V M}^{3}}$
  $J_{3}$ は偏差応力の第3不変量
- シェル要素に対して
  $η$ は応力の3軸性で、 $η = \frac{\frac{1}{3} (σ_{x x} + σ_{y y} + σ_{z z})}{σ_{V M}}$
  $\bar{θ}$ はShift Lode角 $\bar{θ} = 1 - \frac{2}{π} a r \cos ζ$
  で、Lode角（ $θ$ ）パラメータ $ζ = \cos (3 θ) = - \frac{27}{2} η (η^{2} - \frac{1}{3})$
MMC破壊基準による破壊と損傷：
- D = 1の場合：破壊の始まり
- 1 < D <D_cの場合：降伏応力に軟化関数 $β$ が掛けられ、変形抵抗を低減します。
  $σ_{y} = β σ_{y}^{0} {(ε_{p} + ε_{p}^{0})}^{n}$ ここで、 $β = {(\frac{D_{c} - D}{D_{c} - 1})}^{m} 0 < β < 1$
- D ≥ D_cの場合、要素は削除されます。
- 指数部mを使用して軟化の挙動が記述されます。m > 0の使用が推奨されます。
  0 < m < 1の場合、軟化曲線は凸状になります。
  m > 1の場合は凹状になります。軟化は $ε_{f}$ と $D_{c} \cdot ε_{f}$ の間で発生します。塑性ひずみが $D_{c} \cdot ε_{f}$ （この例では $D > D_{c}$ ）に達すると要素が削除されます。
  図 2.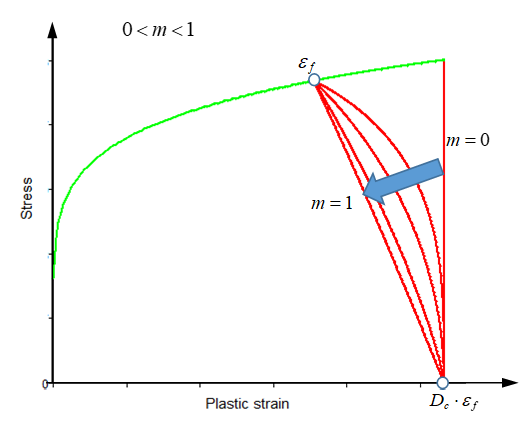
  
  図 3.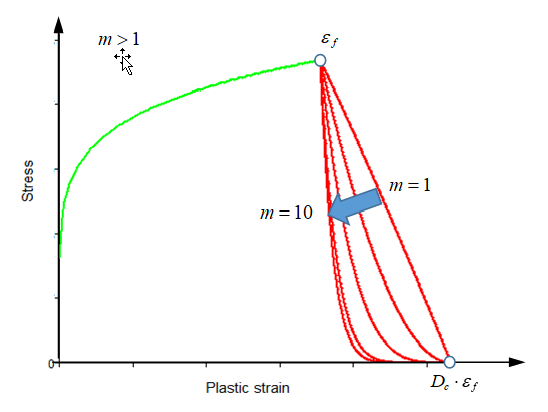
アニメーションファイルにユーザー変数を（Engineの/ANIM/Eltyp/Restypeで）表示可能で、時刻歴ファイルに（Starterの/TH/SHELと/TH/BRIC）で表示可能です：
- USER1：損傷値
/ANIM/BRICK/DAMG、/ANIM/SHELL/DAMG、/H3D/SHELL/DAMGおよび/H3D/SOLID/DAMGを使用して、正規化された損傷変数 $D_{n} = \frac{D}{D_{c}}$ をアニメーションファイルに表示することもできます。

/MAT/LAW72 (HILL_MMC)

フォーマット

定義

例（金属）

コメント