/FAIL/INIEVO
Block Format Keyword This criterion allows a two-step failure approach, divided into an initiation phase, in which damage has no effect on the stress computation, and a damage evolution phase, in which a stress softening can be generated. Initiation is based on plastic strain as function of several stress state quantities.
When the initiation criterion is reached, stress softening damage variable evolution is triggered. This evolution can be based on a plastic displacement at the time of failure or on a certain value of fracture energy. In addition, the shape can be chosen between a classic linear stress reduction or an exponential drop of the load-carrying capacity. Multiple pairs of initiation/evolution criterion can be combined in the same input card. This criterion is compatible with both solids and shells and can be used with non-local regularization.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /FAIL/INIEVO/mat_ID/unit_ID | |||||||||
| NINIEVO | ISHEAR | ILEN | FAILIP | PTHICKFAIL | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| INITYPE | EVOTYPE | EVOSHAP | COMPTYP |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| TAB_ID | SR_REF | FSCALE | PARAM | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| TAB_EL | EL_REF | ELSCAL | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DISP | ALPHA | ENER | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fail_ID |
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | (Optional) Unit
identifier. (Integer, maximum 10 digits) |
|
| NINIEVO | Number of initiation/evolution
criteria. Default = 1 (Integer) |
|
| ISHEAR | Flag to take transverse shear
components into account (shells only).
(Integer) |
|
| ILEN | Element characteristic length
formulation flag.
(Integer) |
|
| FAILIP | Number of failed integration point
prior to solid element deletion. Default = 1 (Integer) |
|
| PTHICKFAIL | Percentage of failed layers prior
to shell element deletion. 0.0 ≤ PTHICKFAIL ≤ 1.0 Default = 0.0 (Real) |
|
| INITYPE | Damage initiation tabulated
criterion type. 2
(Integer) |
|
| EVOTYPE | Damage evolution type.
(Integer) |
|
| EVOSHAP | Shape of the damage evolution.
(Integer) |
|
| COMPTYP | Criterion combination type (only if
NINIEVO > 0).
(Integer) |
|
| TAB_ID | Failure initiation criterion table
identifier. (Integer) |
|
| SR_REF | Reference strain rate for table
identifier. Default = 1.0 (Real) |
|
| FSCALE | Scale factor for failure initiation
criterion table. Default = 1.0 (Real) |
|
| PARAM | Parameter for failure initiation criterion.
Default = 0.0 (Real) |
|
| TAB_EL | Element size scaling for failure
initiation criterion. (Integer) |
|
| EL_REF | Reference element size for size
scaling table. Default = 1.0 (Real) |
|
| ELSCAL | Scale factor for element size
scaling function. Default = 1.0 (Real) |
|
| DISP | Plastic displacement at
failure. Default = 0.0 (Real) |
|
| ALPHA | Exponential shape parameter (not
applicable for exponential energy- based evolution). Default = 1.0 |
|
| ENER | Fracture energy. Default = 0.0 |
|
| fail_ID | (Optional) Failure criteria
identifier. (Integer, maximum 10 digits) |
Comments
- The
INIEVO failure criterion is a two-step failure
criterion based on plastic strain and stress state. These two steps consist
in the computation of two successive damage variables:
- 1st step: the damage initiation phase, in which an internal variable evolution denoted is computed. This variable is a purely internal value that has no influence on the stress computation. Once this initiation variable reaches the value 1.0, the second stage of the failure is triggered by the computation of the damage variable evolution denoted .
- 2nd step: The damage variable evolution is computed, generating a stress softening effect until the complete failure of the element and its deletion.
- Different types of failure
initiation criterion can be used depending on the INITYPE
parameter value.
- If INITYPE = 1: A tabulated
plastic strain at failure initiation map is given with respect to
stress triaxiality and, optionally, with strain rate.Where,
- Hydrostatic pressure
- von Mises stress
- If INITYPE = 2: A tabulated
plastic strain at failure initiation map is given with respect to a
shear influence variable denoted as and, optionally, with strain rate.Where,
- Pressure influence parameter
- Maximum shear stress
- If INITYPE = 3: A tabulated
modified plastic strain at failure initiation map is given with
respect to principal strain rate ratio and, optionally, with strain
rate. This initiation criterion is also denoted as
MSFLD.
Where, are the principal deviatoric stress component.
- If INITYPE = 4: A tabulated
plastic strain at failure initiation map is given with respect to
principal strain rate ratio and, optionally, with strain rate. This
initiation criterion is also denoted as
FLD.
- If INITYPE = 5: A tabulated
plastic strain at failure initiation map is given with respect to a
stress state parameter denoted as
and, optionally, with strain rate. This initiation criterion is
also denoted as
FLD.Important: The strain rate dependency applied to the failure criterion can only be used with material laws that are strain rate dependent. The strain rate used for the constitutive law (total strain rate, deviatoric strain rate or plastic strain rate), will be the same used for the failure criterion.
- If INITYPE = 1: A tabulated
plastic strain at failure initiation map is given with respect to
stress triaxiality and, optionally, with strain rate.
- The damage initiation
variable,
is computed incrementally
as:
- If INITYPE = 3 (MSFLD), a
modified plastic strain is used, which only evolves when
:
- If INITYPE = 3 (MSFLD) and
INITYPE = 4 (FLD) criteria,
depending on PARAM value, a direct formulation
can be used instead of the incremental one:
- If INITYPE = 3 (MSFLD), a
modified plastic strain is used, which only evolves when
:
- To take into account
regularization of the element size, a table (TAB_EL) can
be defined describing a scale factor for the element size denoted as
map with respect to initial element size
and, optionally, the stress state variable
used in the failure initiation criterion depending on
INITYPE value. For instance, if
INITYPE = 2,
. The element size factor is introduced into
the damage initiation variable computation as:
- When the damage initiation
variable
reaches the value 1, the
damage variable evolution
is triggered, generating a stress softening.
This evolution can be either based on:
- Plastic displacement at failure (DISP), denoted , if EVOTYPE = 1.
- Dissipated fracture energy (ENER) denoted , if EVOTYPE = 2.
- EVOSHAP
parameter allows to define the shape of the damage evolution. For both
evolution type (plastic displacement or fracture energy), a linear and an
exponential shape can be chosen.
- If EVOSHAP = 1, the damage
evolution is linear:
- If EVOTYPE = 1: plastic
displacement at failure is directly input with
DISP:Where, is the initial element length.
Figure 1. Linear damage evolution with plastic displacement DISP at failure 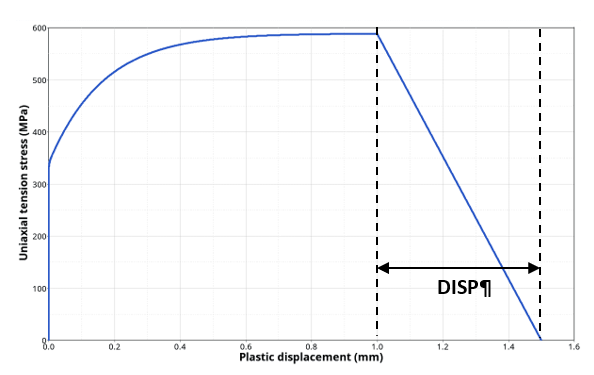
- If EVOTYPE = 2: plastic
displacement at failure is deduced from the fracture energy
input, which is calculated with
ENER:Where, is the yield stress at damage evolution triggering.Note: This expression considers that the plastic behavior is almost perfect at the onset of damage to ensure a dissipated energy equal to .
Figure 2. Linear damage evolution with fracture energy input ENER 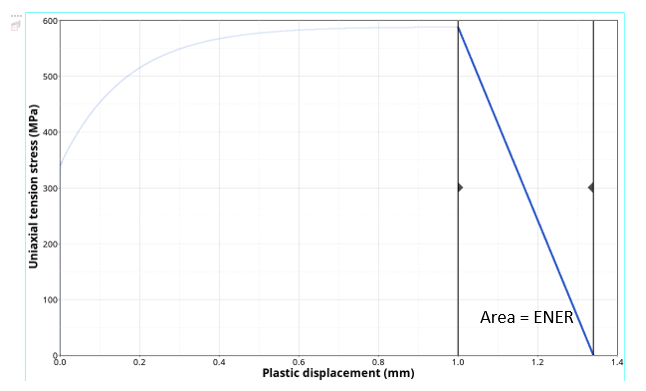
- If EVOTYPE = 1: plastic
displacement at failure is directly input with
DISP:
- If EVOSHAP = 2, the damage
evolution is exponential.
- If EVOTYPE = 1: plastic
displacement at failure is directly input with
DISP and shape of the exponential can
be modified with ALPHA.
Figure 3. Exponential damage evolution with plastic displacement DISP. at failure with different alpha parameter value 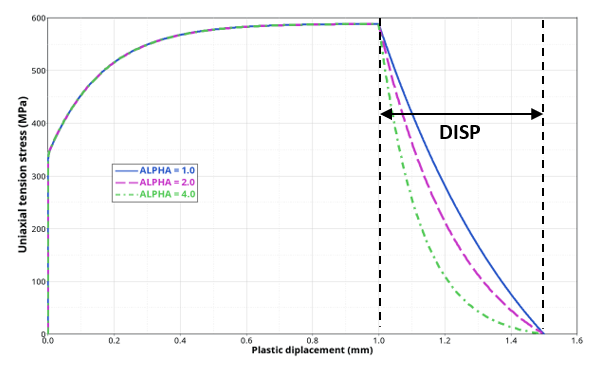
- If EVOTYPE = 2: the area
between the stress – plastic displacement curve of the
exponential function corresponds to the failure energy
ENER.
Figure 4. Exponential damage evolution with fracture energy input ENER 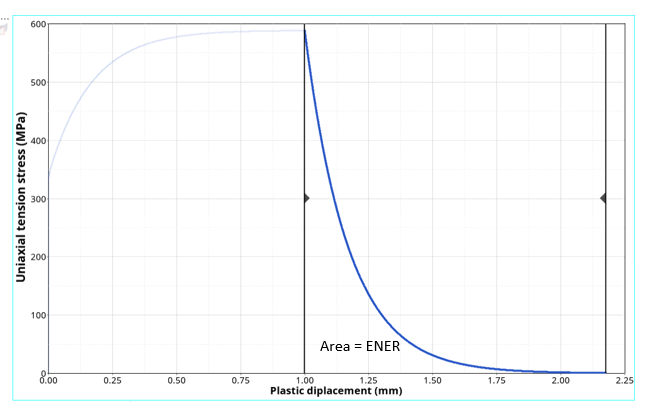
- If EVOTYPE = 1: plastic
displacement at failure is directly input with
DISP and shape of the exponential can
be modified with ALPHA.
- If EVOSHAP = 1, the damage
evolution is linear:
- For the same material,
several pairs of Initiation/Evolution criteria can be defined in the same
input card, setting a value NINIEVO > 1.
In this case, another parameter COMPTYP can be used to
choose the way the different criteria are combined to create the softening effect.
- If COMPTYP = 1: the damage
variable of the criterion concerned, denoted as
, is compared with
the maximum value among all the criteria using
COMPTYP =
1.
Where, is the number of initiation/evolution card using COMPTYP = 1.
- If COMPTYP = 2: the damage
variable of the criterion concerned, denoted as
, is accumulated by a multiplicative
formula among all the criteria using COMPTYP =
2.
Where, is the number of initiation/evolution card using COMPTYP = 2.
Finally, the global damage variable used to calculate the damaged stress tensor is defined as the following maximum value:
Where,- Final damaged stress tensor
- Effective stress tensor (obtained from the material law after plastic return mapping)
- If COMPTYP = 1: the damage
variable of the criterion concerned, denoted as
, is compared with
the maximum value among all the criteria using
COMPTYP =
1.
- FAILIP is an integer value used only for higher order or fully-integrated solid elements. It defines the number of failed integration points before deletion of the solid element.
- The parameter PTHICKFAIL is a real parameter used for shell elements. If PTHICKFAIL is blank or set to 0.0, the value of PTHICKFAIL from the shell property is used. If PTHICKFAIL > 0.0, any PTHICKFAIL value defined in the shell properties are ignored and the value entered in this failure model is used. For values of PTHICKFAIL > 0.0, shell elements fail and are deleted when the ratio of through thickness failed integration points equals or exceeds PTHICKFAIL.
- ILEN
is a flag parameter for you to choose between two possible formulas for
computing the element characteristic length
.
- ILEN=0
- Initial geometrical formulation, where the characteristic length corresponds to the square root of the initial area for shells and the cubic root of initial volume for solids .
- ILEN = 1
- Initial critical timestep formulation where the characteristic length corresponds to the one used to compute the initial element critical timestep. The formula used may vary between the different formulations of shells or solids.
- ILEN = 2
- Current geometrical formulation, where the characteristic length corresponds to the square root of the current area for shells .
- If the non-local regularization is used (/NONLOCAL/MAT), the non-local plastic strain is used to compute the damage initiation variable and the damage variable (and the instability variable if used). Also, in this case, the initial element length in all formula is replaced by the non-local parameter .