RD-E：2201 ALEを用いた着水

ALEアプローチを用いてシミュレートされた単純な試験体の水への衝突。

図 1.


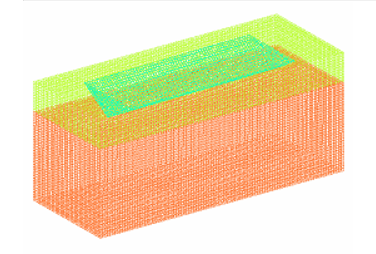
Arbitrary Lagrangian-Eulerian（ALE）アプローチを用いて、三角柱オブジェクトの水槽への着水について検討します。シミュレーション結果は実験結果と解析的結果と比較されます。更に、検討は異なる2つの衝突速度を用いて実行されます。衝撃を与える構造は、三角柱部分です。水はALEメッシュで、構造がLagrangeでモデル化されます。流体-構造間の接触関係は、/INTER/TYPE18を使用してモデル化されます。

使用されるオプションとキーワード

入力ファイル

Before you begin, copy the file(s) used in this example to your working directory.

モデル概要

問題は単純な試験体の水の中への落下から成り、ヘリコプターの着水をシミュレートします。

単位： mm, ms, KN, GPa, kg

三角柱の試験体の水上への衝突が実行され、結果は質的に2の解析的結果、また、Politechnico di Milanoにより得られた実験データとも比較されます。 1

比較は6.7 m/sと11 m/sの2つの衝突速度で実行されます。
図 2. 問題のデータ

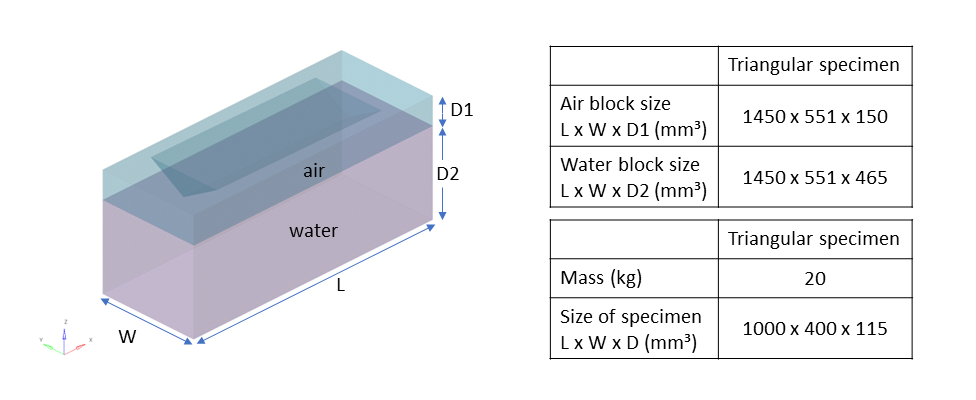
rad_ex_22_law37

衝突三角柱は、平均メッシュサイズが15mm x 15mmのシェル要素を使用してモデル化されています。これは、計算を短縮するために、そのメイン節点に加速度計がある剛体として作成されます。

水は、15x15x15mmのメッシュからなるソリッド要素を使用してモデル化されています。ソリッド要素プロパティ、/PROP/ TYPE14(SOLID)は、EULERプロパティ定式化のIale = 2と一緒に使用されます。

空気と水のモデリングには、推奨されるベストプラクティスである複数の /MAT/LAW6を副材料として使用した/MAT/LAW51を 使用します。例として、/MAT/LAW51を使用したモデルの入力ファイルが含まれています。

1つの/MAT/LAW51カードで、3種類の相を定義できます。この例では、空気と水の2つの相が定義されています。空気は、/MAT/LAW6副材料を使用して以下の特性で定義されます：
  • 初期密度 (Rho_initial) = 1.22e-09 (kg/m³)
  • EoS_Options_Input (IDEAL_GAS)
  • Heat Capacity Ration (Gamma) = 1.4
  • Initial Pressure (P0) = 0.0001 (Pa)
  • Initial Temperature (T0) = 300 (K)
水は、/MAT/LAW6副材料を使用して以下の特性で定義されます：
  • Initial density (Rho_initial) = 1.0 e-06 (kg/m³)
  • EoS_Options_Input (STIFF_GAS)
  • Heat Capacity Ration (Gamma) = 6.1
  • Initial Pressure (P0) = 0.0001 (Pa)
  • EoS Parameter (P_star) = 0.36885
図 3. /MAT/LAW51の材料特性


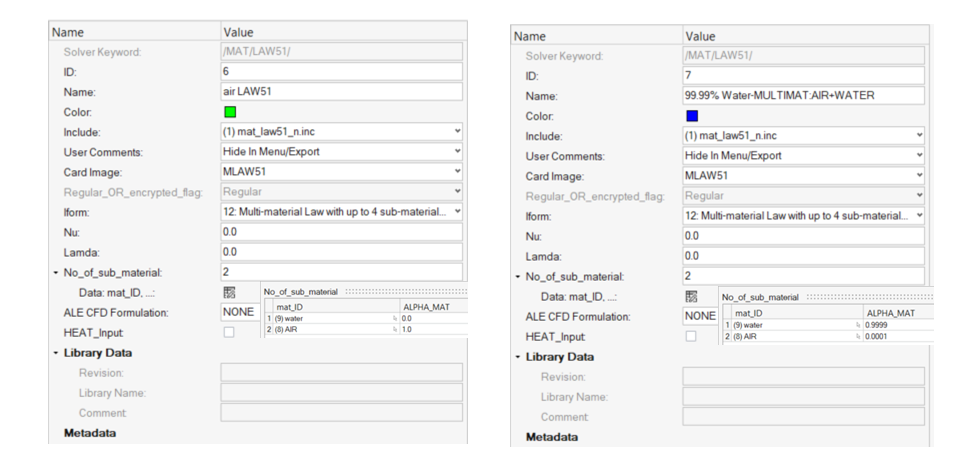
多相材料LAW51では、各副材料の量が定義されています。数値的安定性を向上させるために、水を、99.99%の水と0.01%の空気として定義することを推奨します。

境界の設定

三角柱には初速度と重力がZ方向に加えられます。

境界条件が次のようにALEメッシュに与えられます：
  • X軸に直交する側面はX並進成分を拘束
  • Y軸に直交する側面はY並進成分を拘束
  • 上下面はZ並進成分を拘束
Iform=6としてLAW51を使用すると、パラメータを定義せずにサイレント境界を設定できます。材料パラメータは、その近傍の要素に基づいて計算されます。この場合、要素の1つの層をサイレント境界として定義する必要があります。2つのコーナー境界要素のメッシュを定義することを推奨します（図 4）。
図 4. 境界メッシュの処理


流体-構造連成（FSI）

/INTER/TYPE18インターフェースがLagrangeメッシュ（プリズム）とALE流体の間の接触の取り扱いのために定義されます。衝突三角柱はLagrangianサーフェスであり、ALE流体はALEソリッド要素グループです。

インターフェースTYPE18の力はペナルティ法を使用して計算されます。インターフェース剛性は衝突速度に比例します。ALEアプローチで得られる結果はインターフェースの剛性係数 S t f v a l MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaads hacaWG2bGaamyyaiaadYgaaaa@3A99@ に依存し、これは要素サイズと流体の特性の関数です。

S t f v a l = ρ ⋅ v 2 ⋅ S e l G a p MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaads hacaWG2bGaamyyaiaadYgacqGH9aqpdaWcaaqaaiabeg8aYjabgwSi xlaadAhadaahaaWcbeqaaiaaikdaaaGccqGHflY1caWGtbWaaSbaaS qaaiaadwgacaWGSbaabeaaaOqaaiaadEeacaWGHbGaamiCaaaaaaa@4981@

ここで、
ρ
（最も高い）流体密度
ν
現象の推定相対速度
S e l
Lagrange要素の表面積平均
Gap MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiaadg gacaWGWbaaaa@389D@
接触ギャップ

推奨されるギャップ値は、ALEメッシュの平均要素長の1.5倍です。

水の密度1e-6 kg m m 3 MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaai aadUgacaWGNbaabaGaamyBaiaad2gadaahaaWcbeqaaiaaiodaaaaa aaaa@3C22@ 、速度11 m/s、および平均Lagrangianシェル要素面積を使用すると、次のようになります。

S el =15×15=225 MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGtbWaaS baaSqaaiaadwgacaWGSbaabeaakiabg2da9iaaigdacaaI1aGaey41 aqRaaGymaiaaiwdacaqG9aGaaeOmaiaabkdacaqG1aaaaa@4344@

したがって：

Stfval= 1e−6⋅ 11 2 ⋅225 1.5⋅15 =1.21e−3 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaads hacaWG2bGaamyyaiaadYgacqGH9aqpdaWcaaqaaiaaigdacaWGLbGa eyOeI0IaaGOnaiabgwSixlaaigdacaaIXaWaaWbaaSqabeaacaaIYa aaaOGaeyyXICTaaGOmaiaaikdacaaI1aaabaGaaeymaiaab6cacaqG 1aGaeyyXICTaaeymaiaabwdaaaGaeyypa0Jaaeymaiaab6cacaqGYa GaaeymaiaadwgacqGHsislcaaIZaaaaa@5470@

この例では、パラメータを使用して、衝撃速度とメッシュサイズに応じて S t f v a l MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaads hacaWG2bGaamyyaiaadYgaaaa@3A99@ が自動的に再計算されます。これにより、さまざまな速度の調査が容易になり、これらのパラメータを他のモデルで使用することができます。シミュレーションで入力したパラメータと計算されたパラメータは、Starter出力ファイルに出力されます。
図 5.


結果

図 6. LAW51の密度結果


LAW37およびLAW51を使用したALEシミュレーションの加速度結果は、CFC 60、-3 dBフィルターでフィルタリングされ、Von Karman理論解およびCFC 60, -3 dBフィルターでフィルタリングされた実験結果と比較されました。
図 7. シミュレーション、理論解、および実験テストに対する11 m/sでの加速度結果


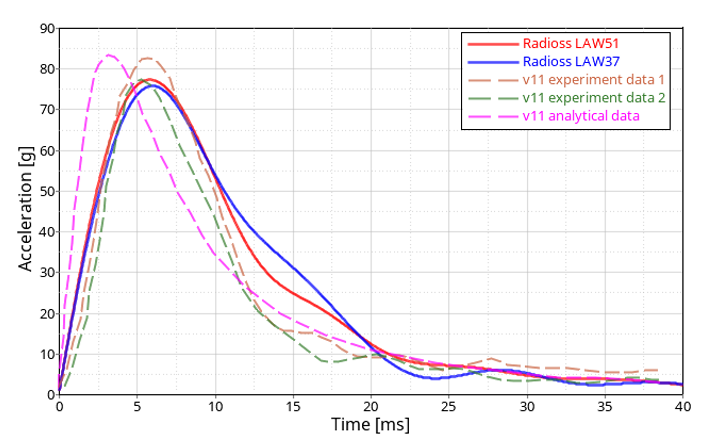
ALE法では、最大加速度はLAW51で77.3g、LAW37で75.8gとなります。しかしながら、Von Karmanの理論解は83.5gで、テストの最大値は82.8gと77.5gの間です。

一般に、ALEの結果は、特に40gを超える加速度の継続時間において、解析と実験の曲線が一致します。流体 - 構造インターフェースの境界でより離散的になるため、 材料LAW51を使用することが推奨されます。