Swept Sine

Some Automotive OEMs refer to this test as a frequency response test. The test is designed to measure the dynamic response of the vehicle to sinusoidal steering input.

Description

This event is designed to work with a full vehicle model that has been built through the MotionView Assembly Wizard. The event should attach to the model automatically when added through the Task Wizard. It can be used with models built manually, as long as the attachment scheme in the event is strictly followed.

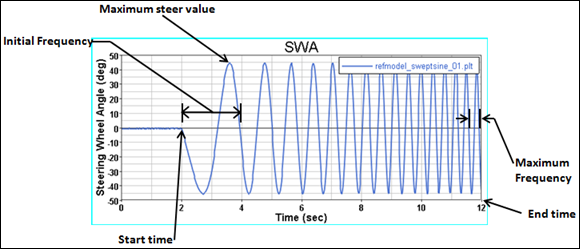
A sinusoidal steering input at the steering wheel determines the frequency response characteristics of the vehicle. The vehicle velocity of 45 mph is kept constant throughout the event. After two seconds, the vehicle steers from its initial value to its maximum steering value, which is 45 degrees with a frequency increase rate of 0.2750 Hz/sec. This event covers a minimum frequency range of 0.25 to 3 Hz. This event helps to determine the steering wheel angle, yaw rate, roll angle, and lateral acceleration.

The initial vehicle velocity, initial and maximum steer value, initial and maximum frequency, frequency rate, start and end time, and time step can be modified via the event form. The wheel rotational velocities are calculated values and should not be changed.

The simplified equation used to define the steering wheel angular input is:

Where,

θ = input steering wheel angle

θ_max = maximum steer value

${\omega }_{init}$ = initial steer frequency

${\omega }_{rate}$ = Frequency rate

time = Simulation time

`{ds_swept_sine.max_str.value}*DTOR
*STEP(TIME, {ds_swept_sine.st_tim.value}, 0.0, {ds_swept_sine.st_tim.value}+0.001, 1.0)
*SIN(2*PI
*(min({ds_swept_sine.max_frq.value},{ds_swept_sine.ini_frq.value}+(({ds_swept_sine.frq_rt.value}/2)
*(TIME-{ds_swept_sine.st_tim.value}))))*(TIME-{ds_swept_sine.st_tim.value}))`

45*DTOR*STEP(TIME, 2, 0.0, 2+0.001, 1.0)*SIN(2*PI*(min(3,0.25+((0.275/2)*(TIME-2))))*(TIME-2))

`{ds_swept_sine.max_str.value}*DTOR

*STEP(TIME, {ds_swept_sine.st_tim.value}, 0.0, {ds_swept_sine.st_tim.value}+0.001, 1.0)

*SIN(2*PI

*(min({ds_swept_sine.max_frq.value},{ds_swept_sine.ini_frq.value}+(({ds_swept_sine.frq_rt.value}/2) *(TIME-{ds_swept_sine.st_tim.value}))))*(TIME-{ds_swept_sine.st_tim.value}))`

Note that the maximum frequency is a frequency limit only. The actual maximum frequency obtained in the simulation is a function of the Initial frequency, the frequency rate, and the start and end time. The steering wheel sine wave begins at the initial frequency at the start time and increases by the frequency rate each second until the event ends at the end time. The maximum frequency only comes in to effect if the end time is mismatched with the frequency rate.

Six types of modeling element containers are used to define the event. Two sub systems (a drive torque controller and output requests) are also included during the event.

Attachments

Datasets

Forms

Joints

Motions

Three motions are included in the event. The steering motion is used in the template which gives the input for the vehicle to steer and acts on a revolute joint that connects the steering wheel to the vehicle body. If a steering column is not included in the model, the motion acts on the joint between the steering rack input shaft and the vehicle body.

The Front and Rear Wheel Motions act on the wheel spindle revolute joints that connect the wheel hub to the knuckle. The motion is initially zero (fixing the wheels to the knuckle) so the model converges statically. The wheel locking motions get deactivated after the convergence of the static analysis to allow the tires to rotate during dynamic analysis.

Solver Variables

Templates

<ResOutput
     angle_type          = "YPR"
  />
  <ResOutput
     mrf_file            = "TRUE"
  />
  <ResOutput
     plt_file            = "TRUE"
  />
  <H3DOutput
     switch_on           = "TRUE"
     increment           = "1"
  />
  <ResOutput
     abf_file            = "TRUE"
  />
{if (tire_dataset.opt_omega.ival ==1)}
<!--Initial static analysis -->

<Simulate
	analysis_type = "Static"
	end_time      = "0.0"
/>	
{endif}

 <Deactivate
	element_type = "MOTION"
	element_id = "{mot_frnt_wheel.l.idstring}"
/>

<Deactivate
	element_type = "MOTION"
	element_id = "{mot_frnt_wheel.r.idstring}"
/>

<Deactivate
	element_type = "MOTION"
	element_id = "{mot_rear_wheel.l.idstring}"
/>

<Deactivate
	element_type = "MOTION"
	element_id = "{mot_rear_wheel.r.idstring}"
/>
{if (tire_dataset.opt_omega.ival ==2)}
<!--Initial static analysis -->

<Simulate
	analysis_type = "Static"
	end_time      = "0.0"
/>	
{endif}
<Deactivate
	element_type = "JPRIM"
	element_id = "{j_clamp_1_body.idstring}"
/>

<Deactivate
	element_type = "JPRIM"
	element_id = "{j_clamp_2_body.idstring}"
/>    

{if ds.inp_type.value == "Angle"}
  <Deactivate
	element_type = "FORCE"
	element_id = "{tor_str.idstring}"
  />
  <Motion_Joint
     id                  = "{wh_motion.idstring}"
     expr                = "IF(TIME-.5:{-ds.str_mag.value}D*STEP(TIME,0,0,0.001,1),{-ds.str_mag.value}D,{-ds.str_rate.value}D*(TIME-.5)-{ds.str_mag.value}D)"
  />                                
                                 
 <Simulate
      analysis_type       = "Transient"
      end_time            = "{(ds.max_str.value-ds.str_mag.value)/ds.str_rate.value+.5}"
      num_steps           = "{((ds.max_str.value-ds.str_mag.value)/ds.str_rate.value+.5)*100}"
  />
 
 {else}
 <Deactivate
 	element_type = "MOTION"
 	element_id = "{wh_motion.idstring}"
/>

<Force_Scalar_TwoBody
     id                  = "{tor_str.idstring}"
     type		 = "Torque"
     val_expression      = "IF(TIME-.5:{-ds.str_mag.value},{-ds.str_mag.value},{-ds.str_rate.value}*(TIME-.5)-{ds.str_mag.value})"
  />
  
  <Simulate
        analysis_type       = "Transient"
        end_time            = "{(ds.max_str.value-ds.str_mag.value)/ds.str_rate.value+.5}"
        num_steps      = "{((ds.max_str.value-ds.str_mag.value)/ds.str_rate.value+.5)*100}"
  />
  {endif}
  
 <Stop/>

References

ISO +7401-2003 - Road vehicles — Lateral transient response test methods — Open-loop test methods.