/MAT/LAW112 (PAPER or XIA)
Block Format Keyword The Paperboard law models an orthotropic and dissymmetric elasto-plastic material from proposed by Xia, 2002.
The basic principle is to fully uncouple the behavior in the plane of the paper sheet and the behavior out of the plane. A yield stress is defined for each directions of loading, in tension and compression.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW112/mat_ID/unit_ID or /MAT/PAPER/mat_ID/unit_ID or /MAT/XIA/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E1 | E2 | E3 | Ires | Itab | Ismooth | ||||
| G12 | G23 | G13 | |||||||
| K | E3C | CC | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| S01 | A01 | B01 | C01 | ||||||
| S02 | A02 | B02 | C02 | ||||||
| S03 | A03 | B03 | C03 | ||||||
| S04 | A04 | B04 | C04 | ||||||
| S05 | A05 | B05 | C05 | ||||||
| ASIG | BSIG | CSIG | |||||||
| TAU0 | ATAU | BTAU | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| TAB_YLD1 | MAT_Xscale1 | MAT_Yscale1 | |||||||
| TAB_YLD2 | MAT_Xscale2 | MAT_Yscale2 | |||||||
| TAB_YLD3 | MAT_Xscale3 | MAT_Yscale3 | |||||||
| TAB_YLD4 | MAT_Xscale4 | MAT_Yscale4 | |||||||
| TAB_YLD5 | MAT_Xscale5 | MAT_Yscale5 | |||||||
| TAB_YLDC | MAT_XscaleC | MAT_YscaleC | |||||||
| TAB_YLDS | MAT_XscaleS | MAT_YscaleS | |||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | (Optional) Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material title. (Character, maximum 100 characters) |
|
| Initial
density. (Real) |
||
| Ei | Young’s modulus in the
ith orthotropic direction. (Real) |
|
| Poisson's ratio related to the
ith and jth orthotropic
direction. (Real) |
||
| Shear modulus related to the
ith and jth orthotropic
direction. (Real) |
||
| Ires | Resolution method for plasticity.
(Integer) |
|
| Itab | Yield stresses computation.
(Integer) |
|
| Ismooth | Interpolation type (in case of
tabulated yield function).
(Integer) |
|
| K | In-plane yield surface
exponent. Default = 1.0 (Real) |
|
| E3C | First elastic compression
parameter. Default = E3 (Real) |
|
| CC | Second elastic compression
parameter. Default = 1.0 (Real) |
|
| Tensile plastic Poisson’s ratio in
direction 1. (Real) |
||
| Tensile plastic Poisson’s ratio in
direction 2. (Real) |
||
| Compressive plastic Poisson’s ratio
in direction 1. (Real) |
||
| Compressive plastic Poisson’s ratio
in direction 2. (Real) |
||
| S0i | Initial yield stress in the
ith direction of loading. Each direction is
associated to a given loading direction following the order:
Default = 1.0e20 (Real) |
|
| A0i | First hardening parameter in the
ith direction of loading. (Real) |
|
| B0i | Second hardening parameter in the
ith direction of loading. (Real) |
|
| C0i | Third hardening parameter in the
ith direction of loading. (Real) |
|
| ASIG | Initial out-of-plane yield stress
in compression. Default = 1.0e20 (Real) |
|
| BSIG | First out-of-plane hardening
parameter in compression. (Real) |
|
| CSIG | Second out-of-plane hardening
parameter in compression. (Real) |
|
| TAU0 | Initial transverse shear yield
stress. Default = 1.0e20 (Real) |
|
| ATAU | First transverse shear hardening
parameter. (Real) |
|
| BTAU | Second transverse shear hardening
parameter. (Real) |
|
| TAB_YLDi | Tabulated yield stress – plastic
strain - strain rate function identifier in the ith
direction of loading. (Integer) |
|
| MAT_Xscalei | X scale factor of the tabulated
yield – plastic strain - strain rate function in the
ith direction of loading. Default = 1.0 (Real) |
|
| MAT_Yscalei | Y scale factor of the tabulated
yield – plastic strain - strain rate function in the
ith direction of loading. Default = 1.0 (Real) |
Example (Paper)
#RADIOSS STARTER
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW112/1/1
Xia
# RHO_I
7.83E-10
# E1 E2 E3 Ires Itab Ismooth
4193 1554 1554 2 0 0
# nu21 G12 G23 G13
0.1011 988 76 76
# K E3C CC
2.0 47.2 24.46
# nu1p nu2p nu4p nu5p
0.555 0.1537 0.18 0.145
# S01 A01 B01 C01
12.0 19.0 260.0 800.0
# S02 A02 B02 C02
6.5 40.0 160.0 250.0
# S03 A03 B03 C03
6.0 11.0 100.0 125.0
# S04 A04 B04 C04
7.3 6.0 160.0 300.0
# S05 A05 B05 C05
6.3 9.0 310.0 225.0
# ASIG BSIG CSIG
16.55 16.55 3.16
# TAU0 ATAU BTAU
2.1 9.0 2.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATAExample (Tabulated)
#RADIOSS STARTER
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW112/1/1
Xia_tab
# RHO_I
7.83E-10
# E1 E2 E3 Ires Itab Ismooth
4193 1554 1554 1 1 1
# nu21 G12 G23 G13
0.1011 988 76 76
# K E3C CC
2.0 47.2 24.46
# nu1p nu2p nu4p nu5p
0.555 0.1537 0.18 0.145
# TAB_YLD1 MAT_Xscale1 MAT_Yscale1
25 1.0 1.0
# TAB_YLD2 MAT_Xscale2 MAT_Yscale2
25 1.0 0.35
# TAB_YLD3 MAT_Xscale3 MAT_Yscale3
25 1.0 0.75
# TAB_YLD4 MAT_Xscale4 MAT_Yscale4
25 1.0 0.6341
# TAB_YLD5 MAT_Xscale5 MAT_Yscale5
25 1.0 0.5
# TAB_YLDC MAT_XscaleC MAT_YscaleC
25 1.0 0.5
# TAB_YLDS MAT_XscaleS MAT_YscaleS
25 1.0 0.5
/FUNCT/46
ecoulement2
# plastic strain stress
0.0 12.00
0.012 32.979020979021
0.025 50.4615384615385
0.05 74.5
0.075 90.9473684210526
0.1 102.909090909091
0.125 112.00
0.15 119.142857142857
0.175 124.903225806452
0.2 129.647058823529
0.25 137.00
0.3 142.434782608696
0.4 149.931034482759
0.5 154.857142857143
1.0 165.846153846154
/TABLE/1/25
Yld Functions : plastic strain + strain rate dependency
#DIMENSION
2
# FCT_ID strain rate Scale_y
46 0.0 1.00
46 1.0 1.10
46 5.0 1.15
46 10.0 1.20
46 100.0 1.25
46 100000.0 1.35
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddataComments
- To describe the
behavior of the paperboard material law, the following orthotropic direction
is considered.
Figure 1. 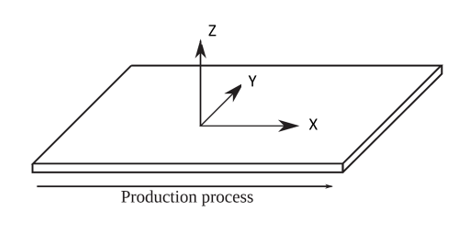
- The elastic behavior
of this material law is orthotropic.
The in-plane behavior should be fully uncoupled with the out-of-plane behavior, computed as:
With
The transverse shear components are computed as:
The out-of-plane elastic behavior (for solids only) is treated as a uniaxial equivalent problem. However, the computation of the stress may differ between tension and compression. The elasticity becomes nonlinear for compressive loadings.
- In the Xia 2002
formulation, the in-plane yield criterion, denoted as
, is defined as:
Where,
- Switching parameters.
- Cauchy stress tensor.
- Normal direction of the yield planes.
- Yield stresses.
- Positive integer.
Each direction is associated to a given loading direction following the order defined below:- 1
- Tension in orthotropic direction 1.
- 2
- Tension in orthotropic direction 2.
- 3
- Positive in-plane shear.
- 4
- Compression in orthotropic direction 1.
- 5
- Compression in orthotropic direction 2.
- 6
- Negative in-plane shear (same input as positive in-plane shear ).
The normal direction vector to the yield planes are:
Each direction is then associated to a specific yield stress whose expression is:
Where, is the in-plane equivalent plastic strain (associated to the yield function ).
The out-of-plane yield function is denoted as is defined as:
with
Where, is the out-of-plane equivalent plastic strain (associated to the yield function ).
The transverse shear yield function is:
Where,- Out-of-plane equivalent plastic strain (associated to the yield function ).
If the tabulated yield stress option is selected (Itab = 1), each yield stress is associated to a table (TAB_YLDi) to define the stress evolution with the plastic strain, at several plastic strain-rate. Two scale factors can be also defined in the X and Y direction for each table. In this case, the hardening parameters , , , , , , , , , and are ignored, and the yield stress becomes:
For output field, an equivalent “global” plastic strain is computed as: