/MAT/LAW72 (HILL_MMC)

Block Format Keyword Describes the anisotropic Hill material with a modified Mohr fracture criteria. This law is available for shell and solid.

Format


(1)	(3)	(5)	(7)	(9)
/MAT/LAW72/`mat_ID`/`unit_ID` or /MAT/HILL_MMC/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	`v`
$σ_{y}^{0}$	$ε_{p}^{0}$	`n`	`F`	`G`
`H`	`N`	`L`	`M`
`C`₁	`C`₂	`C`₃	`m`	`D`_c

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`	Initial Young's modulus. (Real)	$[Pa]$
`v`	Poisson's ratio. (Real)
$σ_{y}^{0}$	Initial yield stress. Default = 10²⁰ (Real)	$[Pa]$
$ε_{p}^{0}$	Initial plastic strain. Default = 10^-20 (Real)
`n`	Exponent for the isotropic function for the swift hardening: $σ_{y} = σ_{y}^{0} {(ε_{p} + ε_{p}^{0})}^{n}$ It is also used as an exponent in the MMC failure equations. 2 Default = 1.0 (Real)
`F`, `G`, `H`, `L`, `M`, `N`	Six HILL Materials anisotropic parameters (> 0). (float)
`C`₁	First parameter for MMC fracture model. (Real)
`C`₂	Second parameter for MMC fracture model. Default = $σ_{y}^{0}$ (Real)	$[Pa]$
`C`₃	Third parameter for MMC fracture model. (Real)
`m`	Exponent for the softening function. 3 Default = 1.0 (Real)
`D`_c	Critical damage. = 1 (Default) The element is deleted when damage reaches one. > 1 The yield stress is modified by using a softening function. 3 If damage reaches the critical damage value, the element is deleted. (Real)

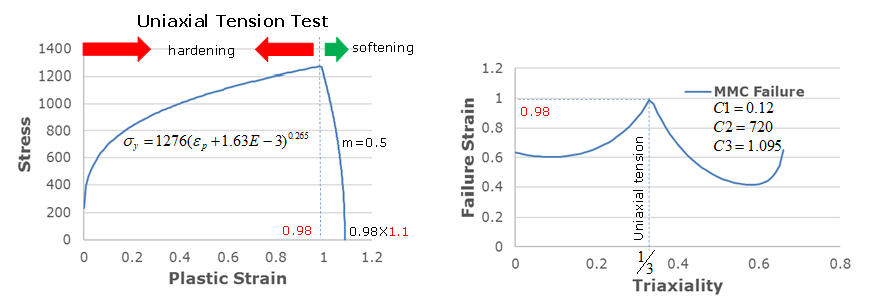
Example (Metal)

Material softening and failure are considered in the material example. Using the MMC parameters C₁, C₂, and C₃ the failure strain in a uniaxial tension test is calculated to be 0.98. In a uniaxial tension test with m=0.5, the material starts to soften at 0.98 until 0.98 x D_c is reached.

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW72/1/1
Metal
#              RHO_I
              0.0028
#                  E                  nu
              200E+3                 0.3
#               Sig0                Eps0                   n                   F                   G
                1276             1.63E-3               0.265                 0.5                 0.5
#                  H                   N                   L                   M
                 0.5                 1.5                   0                   0
#                 C1                  C2                  C3                   m                  Dc
                0.12                 720               1.095                 0.5                 1.1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

3D equivalent Hill stress:
$f = \sqrt{F {(σ_{yy} - σ_{zz})}^{2} + G {(σ_{zz} - σ_{xx})}^{2} + H {(σ_{xx} - σ_{yy})}^{2} + 2 L σ_{yz}^{2} + 2 M σ_{zx}^{2} + 2 N σ_{xy}^{2}}$
For shell element, take:
$f = \sqrt{F σ_{yy}^{2} + G σ_{xx}^{2} + H {(σ_{xx} - σ_{yy})}^{2} + 2 N σ_{xy}^{2}}$
MMC fracture criteria:
$D = \int_{0}^{ε_{p}} \frac{d ε_{p}}{ε_{f} (θ, η)}$
With
$ε_{f} (\bar{θ}, η) = {\frac{σ_{y}^{0}}{C_{2}} [C_{3} + \frac{\sqrt{3}}{2 - \sqrt{3}} (1 - C_{3}) (\sec (\frac{\bar{θ} π}{6}) - 1)] [\sqrt{\frac{1 + C_{1}^{2}}{3}} \cos (\frac{\bar{θ} π}{6}) + C_{1} (η + \frac{1}{3} \sin (\frac{\bar{θ} π}{6}))]}^{- \frac{1}{n}}$
- For 3D solid elements
  $η$ is stress triaxiality with $η = \frac{\frac{1}{3} (σ_{x x} + σ_{y y} + σ_{z z})}{σ_{V M}}$
  $\bar{θ}$ is shift Lode angle $\bar{θ} = 1 - \frac{2}{π} a r \cos ζ$
  with Lode angle ( $θ$ ) parameter $ζ = \cos (3 θ) = \frac{27}{2} \frac{J_{3}}{σ_{V M}^{3}}$
  $J_{3}$ is the third invariant of the deviatoric stress.
- For shell elements
  $η$ is stress triaxiality with $η = \frac{\frac{1}{3} (σ_{x x} + σ_{y y} + σ_{z z})}{σ_{V M}}$
  $\bar{θ}$ is shift Lode angle $\bar{θ} = 1 - \frac{2}{π} a r \cos ζ$
  with Lode angle ( $θ$ ) parameter $ζ = \cos (3 θ) = - \frac{27}{2} η (η^{2} - \frac{1}{3})$
Fracture and damage with MMC fracture criteria:
- When D = 1: fracture initiate
- By 1 < D < D_c: the yield stress is multiplied by softening function $β$ to reduce the deformation resistance.
  $σ_{y} = β σ_{y}^{0} {(ε_{p} + ε_{p}^{0})}^{n}$ with $β = {(\frac{D_{c} - D}{D_{c} - 1})}^{m} 0 < β < 1$
- If D ≥ D_c, the element is deleted.
- The exponent m is used to describe the softening behavior. It is recommended to use m > 0.
  If 0 < m < 1, then the softening curve is convex.
  If m > 1, then the softening curve is concave. The softening is between $ε_{f}$ and $D_{c} \cdot ε_{f}$ . Once the plastic strain is reached $D_{c} \cdot ε_{f}$ (in this case $D > D_{c}$ ), then the element is deleted.
  Figure 2.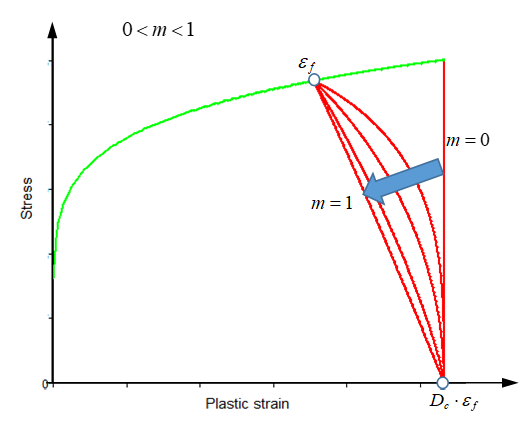
  
  Figure 3.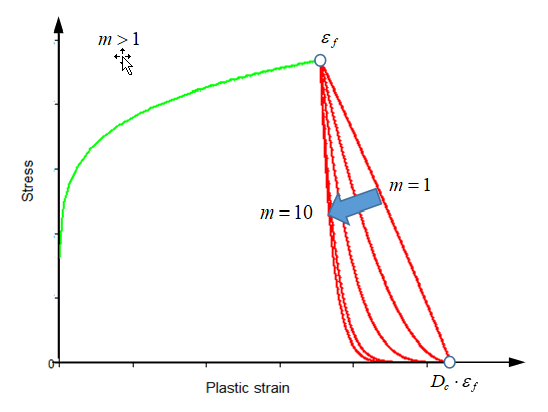
It is possible to display user variables in animation files (with Engine /ANIM/Eltyp/Restype) and in Time history file (with Starter /TH/SHEL and /TH/BRIC):
- USER1: Damage value
It is also possible to display a normalized damage variable $D_{n} = \frac{D}{D_{c}}$ in animation files with /ANIM/BRICK/DAMG, /ANIM/SHELL/DAMG, /H3D/SHELL/DAMG and /H3D/SOLID/DAMG.